Question

$\int \frac{dx}{(\frac{1}{a})^2+x^2}= a^n + tan^{-1}(ax)$. Find the value of n.

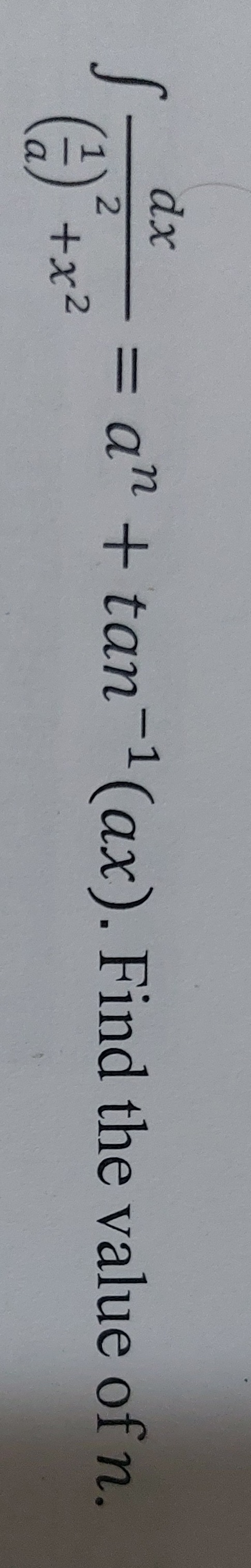
Answer 1

1

Answer 2

We know the standard formula:

$$\int \frac{dx}{x^2+\alpha^2} = \frac{1}{\alpha}\tan^{-1}\left(\frac{x}{\alpha}\right)+C.$$

Here, the integral is

$$\int \frac{dx}{\left(\frac{1}{a}\right)^2+x^2} = \int \frac{dx}{\frac{1}{a^2}+x^2}.$$

Taking $\alpha^2 = \frac{1}{a^2}$ gives $\alpha = \frac{1}{a}$ (assuming $a>0$). Then,

$$\frac{1}{\alpha} = a,$$

and the integral becomes:

$$\int \frac{dx}{\frac{1}{a^2}+x^2} = a\,\tan^{-1}(ax) + C.$$

Comparing with the given form:

$$a^n + \tan^{-1}(ax),$$

we see that the multiplicative factor of $\tan^{-1}(ax)$ must be $a$, i.e., $a^n = a$, which implies:

$$n = 1.$$