Question

$\int \frac{dx}{4x^{2}+4x+2}=$

Answer 1

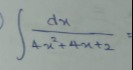
$\frac{1}{2} \tan^{-1}(2x+1) + C$

Answer 2

To evaluate the integral $\int \frac{dx}{4x^{2}+4x+2}$, we will use the method of completing the square in the denominator.

Step 1: Complete the square in the denominator. The denominator is $4x^2+4x+2$. We can factor out 4 from the expression: $4x^2+4x+2 = 4(x^2+x+\frac{1}{2})$

Now, complete the square for the quadratic term inside the parenthesis, $x^2+x+\frac{1}{2}$. To complete the square for $x^2+bx$, we add and subtract $(\frac{b}{2})^2$. Here $b=1$, so we add and subtract $(\frac{1}{2})^2 = \frac{1}{4}$. $x^2+x+\frac{1}{2} = (x^2+x+\frac{1}{4}) - \frac{1}{4} + \frac{1}{2}$ $= (x+\frac{1}{2})^2 + \frac{1}{4}$

Substitute this back into the denominator expression: $4(x^2+x+\frac{1}{2}) = 4\left((x+\frac{1}{2})^2 + \frac{1}{4}\right)$ $= 4(x+\frac{1}{2})^2 + 4 \times \frac{1}{4}$ $= 4(x+\frac{1}{2})^2 + 1$

Step 2: Rewrite the integral with the completed square form. The integral becomes: $\int \frac{dx}{4(x+\frac{1}{2})^2 + 1}$

Step 3: Use substitution to simplify the integral. Let $u = x+\frac{1}{2}$. Then, differentiating both sides with respect to $x$, we get $du = dx$. Substitute $u$ and $du$ into the integral: $\int \frac{du}{4u^2+1}$

Step 4: Prepare the integral for the standard inverse tangent formula. Factor out the coefficient of $u^2$ from the denominator: $\int \frac{du}{4(u^2+\frac{1}{4})} = \frac{1}{4} \int \frac{du}{u^2+\frac{1}{4}}$ We can write $\frac{1}{4}$ as $(\frac{1}{2})^2$: $\frac{1}{4} \int \frac{du}{u^2+(\frac{1}{2})^2}$

Step 5: Apply the standard integral formula. This integral is in the standard form $\int \frac{dx}{x^2+a^2} = \frac{1}{a} \tan^{-1}\left(\frac{x}{a}\right) + C$. In our case, $x$ is $u$ and $a$ is $\frac{1}{2}$. Applying the formula: $\frac{1}{4} \left[ \frac{1}{\frac{1}{2}} \tan^{-1}\left(\frac{u}{\frac{1}{2}}\right) \right] + C$ $= \frac{1}{4} \left[ 2 \tan^{-1}(2u) \right] + C$ $= \frac{1}{2} \tan^{-1}(2u) + C$

Step 6: Substitute back to express the result in terms of $x$. Recall that $u = x+\frac{1}{2}$. Substitute this back into the result: $\frac{1}{2} \tan^{-1}\left(2\left(x+\frac{1}{2}\right)\right) + C$ $= \frac{1}{2} \tan^{-1}(2x+1) + C$

The final answer is $\boxed{\frac{1}{2} \tan^{-1}(2x+1) + C}$.

Explanation of the solution: The integral $\int \frac{dx}{4x^{2}+4x+2}$ is solved by completing the square in the denominator to transform it into the form $a(u^2+k^2)$.

1. The denominator $4x^2+4x+2$ is rewritten as $4(x+\frac{1}{2})^2+1$.
2. A substitution $u = x+\frac{1}{2}$ is made, leading to $\int \frac{du}{4u^2+1}$.
3. This is simplified to $\frac{1}{4} \int \frac{du}{u^2+(\frac{1}{2})^2}$.
4. The standard integral formula $\int \frac{dx}{x^2+a^2} = \frac{1}{a}\tan^{-1}(\frac{x}{a})+C$ is applied with $a=\frac{1}{2}$.
5. The result is $\frac{1}{4} \left( \frac{1}{1/2} \tan^{-1}(\frac{u}{1/2}) \right) + C = \frac{1}{2} \tan^{-1}(2u) + C$.
6. Finally, substituting back $u = x+\frac{1}{2}$ yields $\frac{1}{2} \tan^{-1}(2x+1) + C$.