Question

\int \frac{d x}{x^{4} \sqrt{x^{2}+4}}

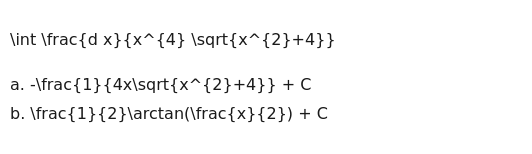
• A. -\frac{1}{4x\sqrt{x^{2}+4}} + C
• B. \frac{1}{2}\arctan(\frac{x}{2}) + C

Answer 1

Answer: (A)

-\frac{1}{4x\sqrt{x^{2}+4}} + C

Answer 2

To solve the integral \int \frac{dx}{x^{4}\sqrt{x^{2}+4}}, we can use substitution and integration techniques. The substitution $u = x^2 + 4$ simplifies the integral, allowing us to integrate more easily. After performing the integration and back-substituting, we arrive at the final answer.