Question

$\int \frac{\cos^4x\,dx}{\sin^3x(\sin^5x + \cos^5x)^{3/5}} = \frac{-1}{2}(1 + (\cot x)^A)^B + C,$

(where $C$ is constant of integration) then $A \times B$ is equal to __________.

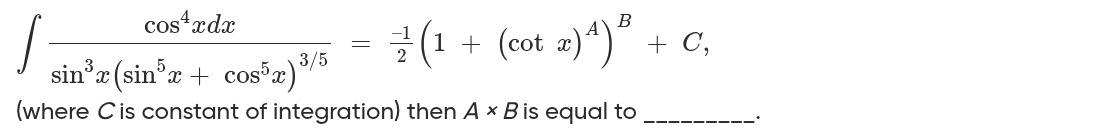
Answer 1

2

Answer 2

1. Manipulate the integrand by dividing the term $(\sin^5x + \cos^5x)^{3/5}$ by $\sin^5x$ to introduce $\cot^5x$.
2. The integrand simplifies to $\cot^4x \csc^2x (1 + \cot^5x)^{-3/5} dx$.
3. Use the substitution $u = 1 + \cot^5x$, leading to $du = -5 \cot^4x \csc^2x dx$.
4. Integrate $-\frac{1}{5} \int u^{-3/5} du$ to get $-\frac{1}{2} u^{2/5} + C$.
5. Substitute back $u$ to obtain $-\frac{1}{2} (1 + \cot^5x)^{2/5} + C$.
6. Comparing with the given form, $A=5$ and $B=2/5$.
7. Calculate $A \times B = 5 \times \frac{2}{5} = 2$.