Question

$\int \frac{cos2x}{cos^2x sin^2x}dx$

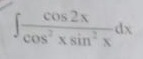
Answer 1

-\cot x - \tan x + C

Answer 2

Solution:

1. Write the integrand using an identity:

   $$\cos2x = \cos^2x - \sin^2x$$

   Substitute into the original integrand:

   $$\frac{\cos2x}{\cos^2x\, \sin^2x} = \frac{\cos^2x - \sin^2x}{\cos^2x\, \sin^2x} = \frac{1}{\sin^2x} - \frac{1}{\cos^2x} = \csc^2x - \sec^2x.$$

2. Integrate term by term:

   $$\int (\csc^2x - \sec^2x)\,dx = \int \csc^2x\,dx - \int \sec^2x\,dx.$$

   We know that:

   $$\int \csc^2x\,dx = -\cot x \quad \text{and} \quad \int \sec^2x\,dx = \tan x.$$

3. Combine the results:

   $$\int \frac{\cos2x}{\cos^2x\, \sin^2x}\,dx = -\cot x - \tan x + C.$$

Minimal Explanation:

• Express $\cos2x$ as $\cos^2x - \sin^2x$.
• Rewrite the integrand as $\csc^2x - \sec^2x$.
• Integrate to obtain $-\cot x - \tan x + C$.