Question
Question: $\int \frac{cos^2x + sin2x}{(2cosx - sinx)^2}dx$...
∫(2cosx−sinx)2cos2x+sin2xdx
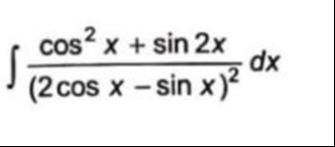
−52ln∣tanx−2∣−tanx−21+52ln∣secx∣−51x+C
Solution
The given integral is I=∫(2cosx−sinx)2cos2x+sin2xdx.
Step 1: Simplify the numerator using sin2x=2sinxcosx. Numerator =cos2x+2sinxcosx.
Step 2: Divide both the numerator and the denominator by cos2x. I=∫cos2x(2cosx−sinx)2cos2xcos2x+2sinxcosxdx I=∫(cosx2cosx−sinx)21+2tanxdx I=∫(2−tanx)21+2tanxdx.
Step 3: Substitute t=tanx. Then dt=sec2xdx=(1+tan2x)dx=(1+t2)dx. So, dx=1+t2dt. Substituting these into the integral: I=∫(2−t)21+2t⋅1+t2dt=∫(t−2)2(t2+1)2t+1dt.
Step 4: Perform partial fraction decomposition for the integrand (t−2)2(t2+1)2t+1. Let (t−2)2(t2+1)2t+1=t−2A+(t−2)2B+t2+1Ct+D. Multiplying by (t−2)2(t2+1): 2t+1=A(t−2)(t2+1)+B(t2+1)+(Ct+D)(t−2)2.
To find coefficients:
-
Set t=2: 2(2)+1=A(0)+B(22+1)+(Ct+D)(0) 5=5B⟹B=1.
-
Compare coefficients of t3: LHS has 0t3. RHS has A(t3)+C(t)(t2)=(A+C)t3. So, A+C=0⟹C=−A.
-
Compare coefficients of t2: LHS has 0t2. RHS has A(−2t2)+B(t2)+C(−4t2)+D(t2)=(−2A+B−4C+D)t2. So, −2A+B−4C+D=0. Substitute B=1 and C=−A: −2A+1−4(−A)+D=0 −2A+1+4A+D=0 2A+D+1=0.
-
Compare constant terms (set t=0): LHS has 1. RHS has A(−2)(1)+B(1)+D(−2)2=−2A+B+4D. So, 1=−2A+B+4D. Substitute B=1: 1=−2A+1+4D⟹0=−2A+4D⟹A=2D.
Now we have a system of equations for A and D: (1) 2A+D+1=0 (2) A=2D Substitute (2) into (1): 2(2D)+D+1=0 4D+D+1=0⟹5D=−1⟹D=−51. From A=2D, A=2(−51)=−52. From C=−A, C=−(−52)=52.
So, the partial fraction decomposition is: (t−2)2(t2+1)2t+1=t−2−2/5+(t−2)21+t2+1(2/5)t−1/5 =−5(t−2)2+(t−2)21+51t2+12t−1.
Step 5: Integrate each term. I=∫(−5(t−2)2+(t−2)21+51t2+12t−1)dt I=−52∫t−21dt+∫(t−2)−2dt+51∫t2+12tdt−51∫t2+11dt I=−52ln∣t−2∣−t−21+51ln(t2+1)−51arctant+C.
Step 6: Substitute back t=tanx. I=−52ln∣tanx−2∣−tanx−21+51ln(tan2x+1)−51arctan(tanx)+C. Using tan2x+1=sec2x and arctan(tanx)=x: I=−52ln∣tanx−2∣−tanx−21+51ln(sec2x)−51x+C I=−52ln∣tanx−2∣−tanx−21+52ln∣secx∣−51x+C.
