Question

$\int \frac{4x}{\sqrt{2x^2-1}} \, dx$

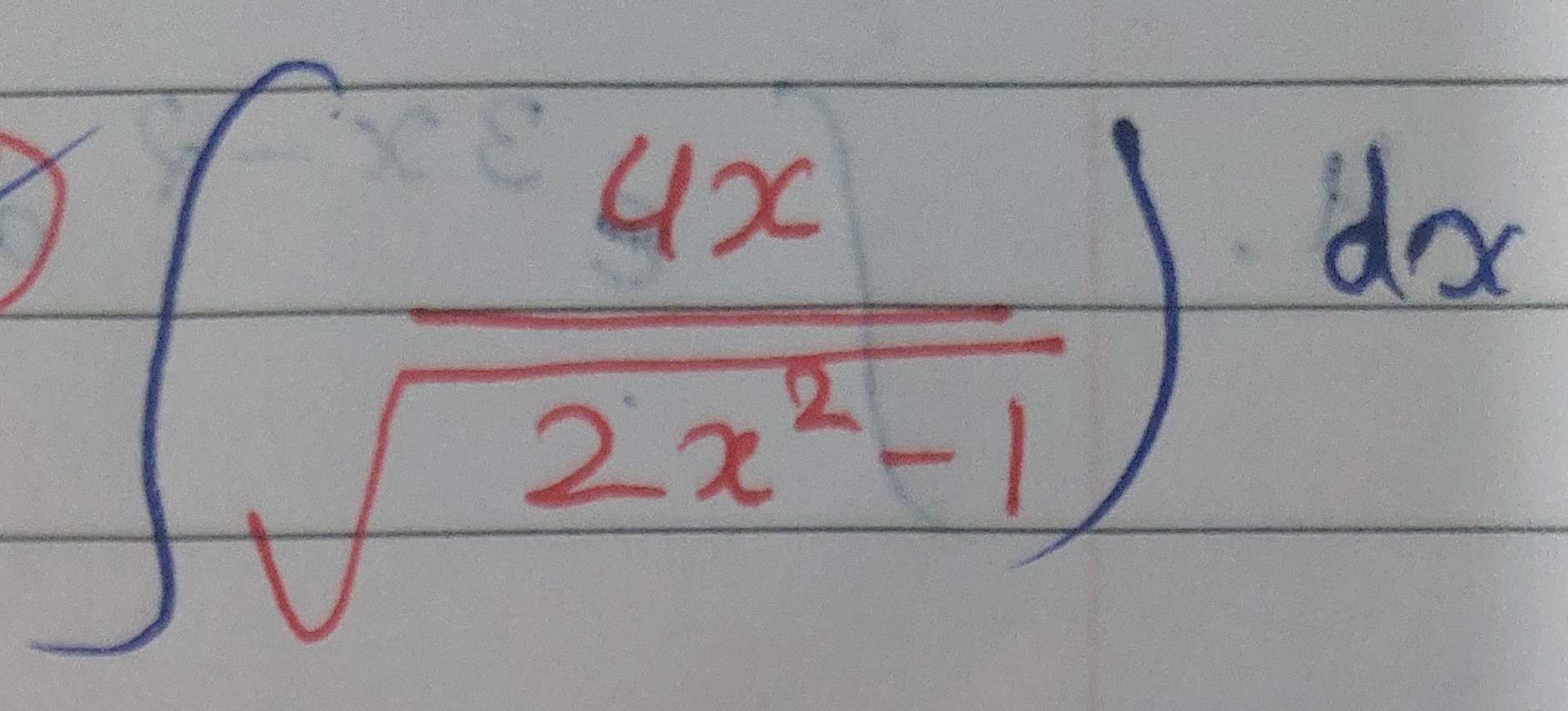
Answer 1

$2\sqrt{2x^2-1} + C$

Answer 2

Let $u = 2x^2 - 1$. Then, $du = 4x \, dx$.

Substitute into the integral:

$\int \frac{4x}{\sqrt{2x^2-1}} \, dx = \int \frac{1}{\sqrt{u}} \, du$.

Integrate:

$\int u^{-1/2} \, du = 2u^{1/2} + C$.

Substitute back:

$2\sqrt{2x^2-1} + C$.

Explanation (Minimal):

Substitution $u = 2x^2-1$ makes $du = 4x \, dx$ and the integral simplifies to $\int u^{-1/2} \, du$, which integrates to $2\sqrt{u}+C$.