Question
Question: $\int \frac{3e^x + 5e^{-x}}{4e^x - 5e^{-x}}dx = Ax + B \ln |4e^{2x} - 5| + C$ the...
∫4ex−5e−x3ex+5e−xdx=Ax+Bln∣4e2x−5∣+C the
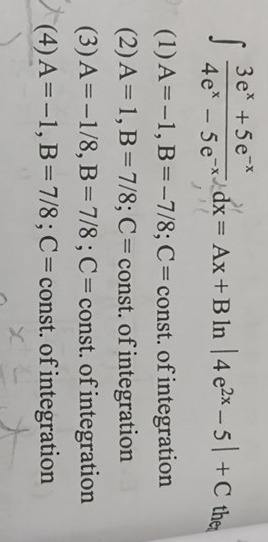
A=-1, B=-7/8; C = const. of integration
A = 1, B = 7/8; C = const. of integration
A=-1/8, B = 7/8; C = const. of integration
A=-1, B=7/8; C = const. of integration
(4)
Solution
To solve the integral I=∫4ex−5e−x3ex+5e−xdx, we express the numerator as a linear combination of the denominator and its derivative.
Let D(x)=4ex−5e−x, then D′(x)=4ex+5e−x.
We want to find λ and μ such that 3ex+5e−x=λ(4ex−5e−x)+μ(4ex+5e−x). This gives us the equations:
4λ+4μ=3 and −5λ+5μ=5.
Solving this system, we find λ=−1/8 and μ=7/8.
Thus, I=∫4ex−5e−x−81(4ex−5e−x)+87(4ex+5e−x)dx=−81∫dx+87∫4ex−5e−x4ex+5e−xdx.
The second integral is 87ln∣4ex−5e−x∣. So, I=−81x+87ln∣4ex−5e−x∣+C.
Since ln∣4ex−5e−x∣=ln∣e−x(4e2x−5)∣=−x+ln∣4e2x−5∣, we have
I=−81x+87(−x+ln∣4e2x−5∣)+C=−x+87ln∣4e2x−5∣+C.
Comparing with Ax+Bln∣4e2x−5∣+C, we get A=−1 and B=7/8.
