Question

$\int \frac{2x\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx$

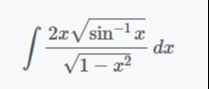
Answer 1

Non-elementary integral

Answer 2

The integral is $\int \frac{2x\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx$.

Substitute $u = \sin^{-1}x$. This implies $x = \sin u$ and $du = \frac{1}{\sqrt{1-x^2}}dx$.

The integral transforms to $\int 2(\sin u)\sqrt{u} du$.

This integral, $\int 2\sqrt{u}\sin u du$, is a non-elementary integral and cannot be expressed in terms of a finite combination of elementary functions.

Answer: The integral is a non-elementary integral.