Question

$\int \frac{2-\tan x}{3+\tan x} dx =$

Answer 1

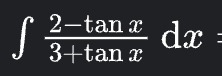
$\frac{1}{2}x + \frac{1}{2} \ln|3\cos x + \sin x| + C$

Answer 2

The problem asks us to evaluate the integral $\int \frac{2-\tan x}{3+\tan x} dx$.

1. Rewrite the integrand in terms of sine and cosine:

The first step is to express $\tan x$ as $\frac{\sin x}{\cos x}$ in the integrand:

$\frac{2-\tan x}{3+\tan x} = \frac{2-\frac{\sin x}{\cos x}}{3+\frac{\sin x}{\cos x}} = \frac{\frac{2\cos x - \sin x}{\cos x}}{\frac{3\cos x + \sin x}{\cos x}} = \frac{2\cos x - \sin x}{3\cos x + \sin x}$

So the integral becomes:

$I = \int \frac{2\cos x - \sin x}{3\cos x + \sin x} dx$

2. Express the numerator as a linear combination of the denominator and its derivative:

This is a standard technique for integrals of the form $\int \frac{A\cos x + B\sin x}{C\cos x + D\sin x} dx$. Let the numerator be $N(x) = 2\cos x - \sin x$ and the denominator be $D(x) = 3\cos x + \sin x$. The derivative of the denominator is $D'(x) = \frac{d}{dx}(3\cos x + \sin x) = -3\sin x + \cos x$.

We want to find constants $\lambda$ and $\mu$ such that $N(x) = \lambda D(x) + \mu D'(x)$.

$2\cos x - \sin x = \lambda (3\cos x + \sin x) + \mu (\cos x - 3\sin x)$

$2\cos x - \sin x = (3\lambda + \mu)\cos x + (\lambda - 3\mu)\sin x$

Comparing the coefficients of $\cos x$ and $\sin x$ on both sides:

For $\cos x$: $3\lambda + \mu = 2 \quad \cdots(1)$

For $\sin x$: $\lambda - 3\mu = -1 \quad \cdots(2)$

From equation (2), we can express $\lambda = 3\mu - 1$. Substitute this into equation (1):

$3(3\mu - 1) + \mu = 2$

$9\mu - 3 + \mu = 2$

$10\mu = 5$

$\mu = \frac{5}{10} = \frac{1}{2}$

Now substitute the value of $\mu$ back into the expression for $\lambda$:

$\lambda = 3\left(\frac{1}{2}\right) - 1 = \frac{3}{2} - 1 = \frac{1}{2}$

So, the numerator can be written as:

$2\cos x - \sin x = \frac{1}{2}(3\cos x + \sin x) + \frac{1}{2}(\cos x - 3\sin x)$

3. Substitute back into the integral and integrate:

Now, substitute this expression for the numerator back into the integral:

$I = \int \frac{\frac{1}{2}(3\cos x + \sin x) + \frac{1}{2}(\cos x - 3\sin x)}{3\cos x + \sin x} dx$

$I = \int \left( \frac{1}{2} + \frac{1}{2} \frac{\cos x - 3\sin x}{3\cos x + \sin x} \right) dx$

We can split this into two simpler integrals:

$I = \frac{1}{2} \int 1 \, dx + \frac{1}{2} \int \frac{\cos x - 3\sin x}{3\cos x + \sin x} dx$

The first integral is straightforward: $\frac{1}{2} \int 1 \, dx = \frac{1}{2}x$.

For the second integral, let $u = 3\cos x + \sin x$. Then, $du = (-3\sin x + \cos x) dx = (\cos x - 3\sin x) dx$. So the second integral becomes:

$\frac{1}{2} \int \frac{1}{u} du = \frac{1}{2} \ln|u| + C' = \frac{1}{2} \ln|3\cos x + \sin x| + C'$

Combining both parts, the complete integral is:

$I = \frac{1}{2}x + \frac{1}{2} \ln|3\cos x + \sin x| + C$

where $C$ is the constant of integration.