Question

$\int \frac{1+x^2}{1+x^4}dx = \frac{1}{\sqrt{2}} tan^{-1} \left[ \frac{f(x)}{\sqrt{2}} \right] + c$, then f(x) =

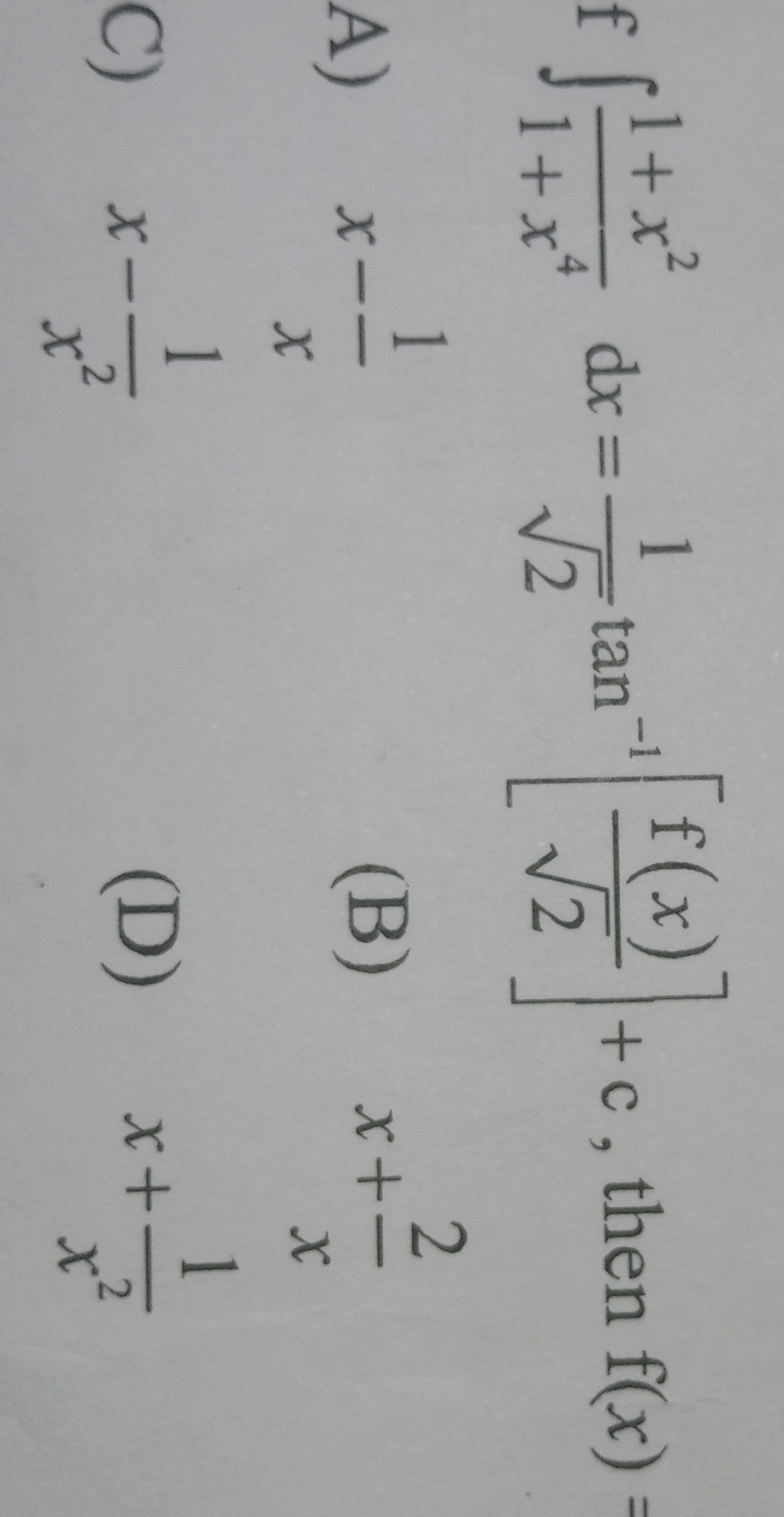
• A. $x - \frac{1}{x}$
• B. $x + \frac{2}{x}$
• C. $x - \frac{1}{x^2}$
• D. $x + \frac{1}{x^2}$

Answer 1

Answer: (A)

$x-\frac{1}{x}$

Answer 2

Step-by-step Solution:

1. Substitution Insight:
   Let

   $$u = x - \frac{1}{x} \quad \Rightarrow \quad \frac{du}{dx} = 1 + \frac{1}{x^2}.$$

   Notice that the numerator in the integrand is $1 + x^2$. After a little algebra, you can see that multiplying $1+1/x^2$ by $x^2$ gives $x^2 + 1$.

2. Form Matching:
   Also note that:

   $$u^2 = \left(x - \frac{1}{x}\right)^2 = x^2 - 2 + \frac{1}{x^2} \quad \Rightarrow \quad u^2+2 = x^2+\frac{1}{x^2}.$$

   With these observations, when differentiating

   $$\frac{1}{\sqrt{2}} \tan^{-1}\left(\frac{u}{\sqrt{2}}\right),$$

   you indeed get a derivative proportional to

   $$\frac{1+x^2}{1+x^4}.$$

3. Verification:
   A quick verification shows that if $f(x)=x-\frac{1}{x}$, then differentiating

   $$\frac{1}{\sqrt{2}} \tan^{-1}\left(\frac{x-1/x}{\sqrt{2}}\right)$$

   reproduces the integrand $\frac{1+x^2}{1+x^4}$.

Thus, the function $f(x)$ is:

$$x-\frac{1}{x}$$