Question
Question: $\int \frac{1+cos^2x}{1+cos^2 2x} dx$...
∫1+cos22x1+cos2xdx
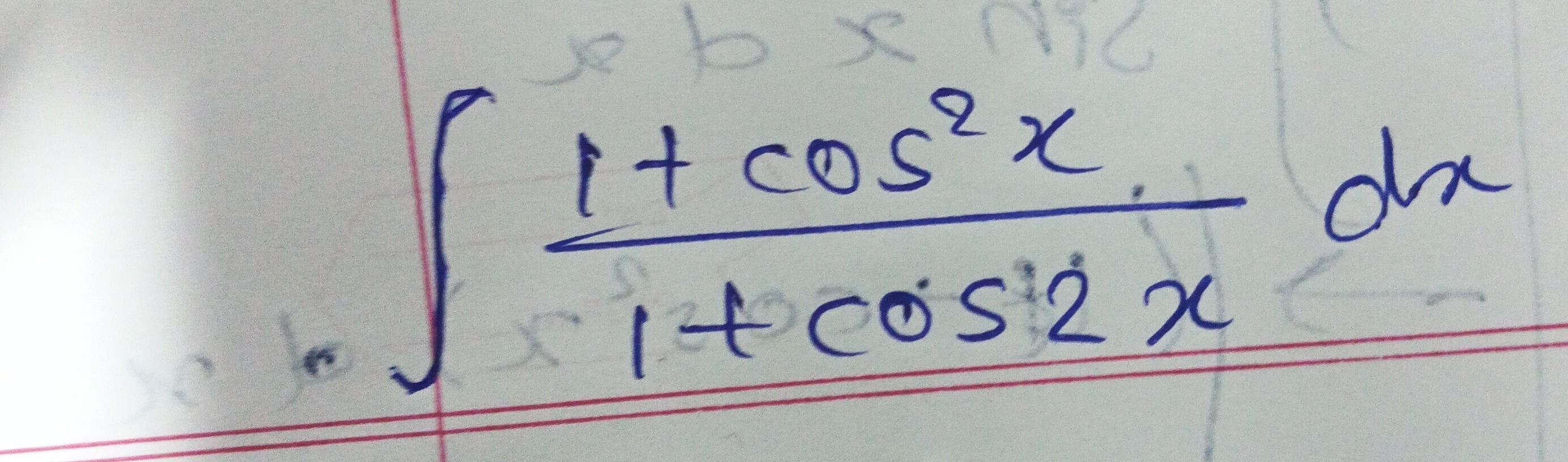
832tan−1(2tan2x)+162ln2−sin2x2+sin2x+C
Solution
The integral to solve is ∫1+cos22x1+cos2xdx.
Step 1: Simplify the numerator using trigonometric identities. We know that cos2x=21+cos2x. Substitute this into the numerator: 1+cos2x=1+21+cos2x=22+1+cos2x=23+cos2x.
Step 2: Rewrite the integral. The integral becomes: ∫1+cos22x23+cos2xdx=21∫1+cos22x3+cos2xdx.
Step 3: Use substitution to simplify the argument of trigonometric functions. Let u=2x. Then du=2dx, which implies dx=21du. Substitute u and dx into the integral: 21∫1+cos2u3+cosu21du=41∫1+cos2u3+cosudu.
Step 4: Split the integral into two parts. 41∫(1+cos2u3+1+cos2ucosu)du.
Step 5: Evaluate the first part of the integral. Let I1=∫1+cos2u3du. Divide the numerator and denominator by cos2u: I1=∫1/cos2u+13/cos2udu=∫sec2u+13sec2udu. Use the identity sec2u=1+tan2u: I1=∫(1+tan2u)+13sec2udu=∫2+tan2u3sec2udu. Now, let t=tanu. Then dt=sec2udu. I1=∫2+t23dt=3∫(2)2+t2dt. This is a standard integral of the form ∫a2+x2dx=a1tan−1(ax). I1=3⋅21tan−1(2t)=23tan−1(2tanu).
Step 6: Evaluate the second part of the integral. Let I2=∫1+cos2ucosudu. Let v=sinu. Then dv=cosudu. Also, cos2u=1−sin2u=1−v2. Substitute these into the integral: I2=∫1+(1−v2)dv=∫2−v2dv. This is a standard integral of the form ∫a2−x2dx=2a1lna−xa+x. Here a=2. I2=221ln2−v2+v. Substitute back v=sinu: I2=221ln2−sinu2+sinu.
Step 7: Combine the results and substitute back u=2x. The total integral is 41(I1+I2). ∫1+cos22x1+cos2xdx=41[23tan−1(2tanu)+221ln2−sinu2+sinu]+C. Substitute u=2x: =41[23tan−1(2tan2x)+221ln2−sin2x2+sin2x]+C. Simplify the coefficients: =423tan−1(2tan2x)+821ln2−sin2x2+sin2x+C. Rationalize the denominators (optional, but often preferred): =832tan−1(2tan2x)+162ln2−sin2x2+sin2x+C.
The final answer is 832tan−1(2tan2x)+162ln2−sin2x2+sin2x+C.
