Question
Question: $\int \frac{1}{(a + b \cos x)^2}dx, a>b>0$...
∫(a+bcosx)21dx,a>b>0
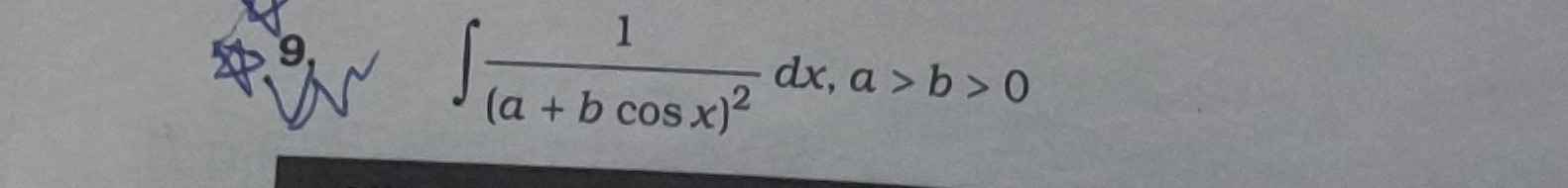
(a2−b2)3/22aarctan(a+ba−btan(x/2))−(a2−b2)(a+bcosx)bsinx+C
Solution
To evaluate the integral I=∫(a+bcosx)21dx, where a>b>0, we can use a standard technique for integrals of the form ∫(A+Bcosx)n1dx.
-
Use a clever algebraic manipulation:
We know that dxd(a+bcosxsinx)=(a+bcosx)2cosx(a+bcosx)−sinx(−bsinx)=(a+bcosx)2acosx+bcos2x+bsin2x=(a+bcosx)2acosx+b.
So, ∫(a+bcosx)2acosx+bdx=a+bcosxsinx. -
Rewrite the numerator of the integrand:
We want to integrate (a+bcosx)21. We can express the numerator 1 in terms of a+bcosx and acosx+b.
Consider the identity: a(a+bcosx)−b(acosx+b)=a2+abcosx−abcosx−b2=a2−b2.
Since a>b>0, a2−b2=0.
So, 1=a2−b21[a(a+bcosx)−b(acosx+b)]. -
Substitute and split the integral:
Substitute this expression for 1 into the integral:
I=∫a2−b21[(a+bcosx)2a(a+bcosx)−b(acosx+b)]dx
I=a2−b21∫[(a+bcosx)2a(a+bcosx)−(a+bcosx)2b(acosx+b)]dx
I=a2−b21[a∫a+bcosx1dx−b∫(a+bcosx)2acosx+bdx] -
Evaluate the two resulting integrals:
We already know the second integral: ∫(a+bcosx)2acosx+bdx=a+bcosxsinx.
For the first integral, ∫a+bcosx1dx, we use the substitution t=tan(x/2).
Then dx=1+t22dt and cosx=1+t21−t2.
∫a+bcosx1dx=∫a+b1+t21−t211+t22dt
=∫a(1+t2)+b(1−t2)1+t21+t22dt=∫a+at2+b−bt22dt=∫(a−b)t2+(a+b)2dt
=a−b2∫t2+a−ba+bdt=a−b2∫t2+(a−ba+b)2dt
This is of the form ∫x2+k21dx=k1arctan(kx).
So, ∫a+bcosx1dx=a−b2a−ba+b1arctan(a−ba+bt)
=(a−b)(a+b)2arctan(ta+ba−b)=a2−b22arctan(a+ba−btan(x/2)). -
Combine the results:
Substitute these back into the expression for I:
I=a2−b21[a(a2−b22arctan(a+ba−btan(x/2)))−b(a+bcosxsinx)]+C
I=(a2−b2)3/22aarctan(a+ba−btan(x/2))−(a2−b2)(a+bcosx)bsinx+C.
The final answer is (a2−b2)3/22aarctan(a+ba−btan(x/2))−(a2−b2)(a+bcosx)bsinx+C.
Explanation of the solution:
- Recognize the integral form.
- Use the identity dxd(a+bcosxsinx)=(a+bcosx)2acosx+b.
- Rewrite the numerator of the integrand: 1=a2−b21[a(a+bcosx)−b(acosx+b)].
- Substitute and split the integral into two parts:
- a∫a+bcosx1dx
- −b∫(a+bcosx)2acosx+bdx
- The second integral is directly solved using the derivative identity.
- The first integral is solved using the substitution t=tan(x/2), which transforms it into a standard integral of the form ∫t2+k21dt.
- Combine the results of the two integrals to get the final solution.
