Question

$\int \frac{1}{1-2x} dx$

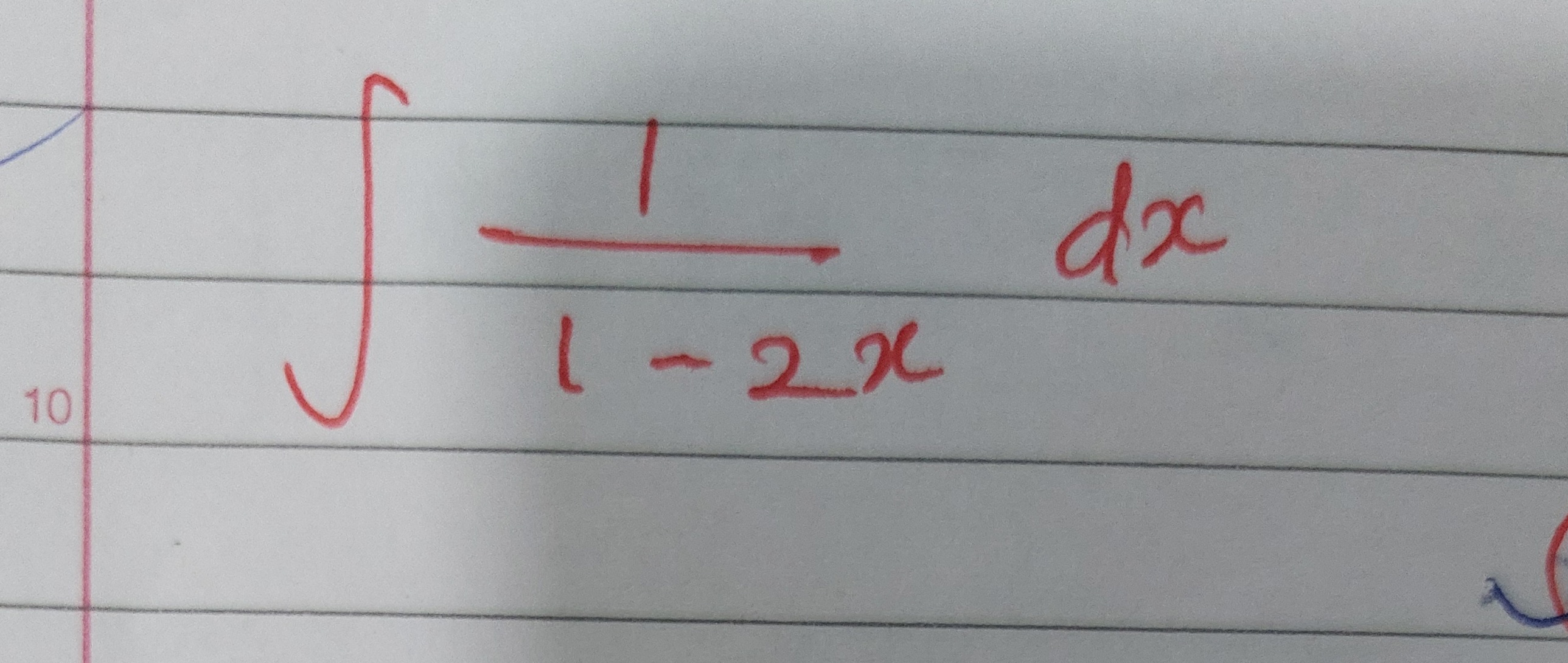
Answer 1

$-\frac{1}{2}\ln|1-2x|+C$

Answer 2

Let

$u = 1-2x \quad \Rightarrow \quad du = -2\,dx \quad \Rightarrow \quad dx = -\frac{1}{2}\,du$.

Substitute in the integral:

$\int \frac{1}{1-2x}\,dx = \int \frac{1}{u}\left(-\frac{1}{2}\,du\right) = -\frac{1}{2}\int \frac{du}{u} = -\frac{1}{2}\ln|u|+C$.

Substitute back for $u$:

$-\frac{1}{2}\ln|1-2x|+C$.

Core Explanation:
Substitute $u=1-2x$, then integrate $\int \frac{du}{u}$, and resubstitute to obtain the result.