Question
Question: $\int \frac{1-x^7}{x(1+x^7)}dx$ equals -...
∫x(1+x7)1−x7dx equals -
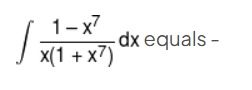
ln∣x∣−72ln∣1+x7∣+C
Solution
To evaluate the integral ∫x(1+x7)1−x7dx, we can use the method of substitution followed by partial fraction decomposition.
-
Substitution: Let t=x7.
Differentiating both sides with respect to x:
dt=7x6dx
This implies dx=7x6dt.Now, substitute t and dx into the integral: ∫x(1+x7)1−x7dx=∫x(1+t)1−t(7x6dt) =∫7x7(1+t)1−tdt Since x7=t, we can replace x7 in the denominator: =∫7t(1+t)1−tdt =71∫t(1+t)1−tdt
-
Partial Fraction Decomposition: Now, we need to decompose the rational function t(1+t)1−t into partial fractions.
Let: t(1+t)1−t=tA+1+tB Multiply both sides by t(1+t):
1−t=A(1+t)+Bt To find A: Set t=0:
1−0=A(1+0)+B(0)
1=ATo find B: Set t=−1:
1−(−1)=A(1−1)+B(−1)
2=0−B
B=−2So, the partial fraction decomposition is: t(1+t)1−t=t1−1+t2
-
Integration: Substitute the partial fractions back into the integral: 71∫(t1−1+t2)dt Integrate each term: =71(∫t1dt−∫1+t2dt) =71(ln∣t∣−2ln∣1+t∣)+C
-
Substitute back t=x7: =71(ln∣x7∣−2ln∣1+x7∣)+C Using the logarithm property ln(ab)=bln(a): =71(7ln∣x∣−2ln∣1+x7∣)+C Distribute the 71: =ln∣x∣−72ln∣1+x7∣+C
