Question
Question: $\int \frac{(1-t)^2}{(1+t)^4} dt$...
∫(1+t)4(1−t)2dt
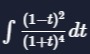
−61(1+t1−t)3+C
Solution
Let the integral be I.
I=∫(1+t)4(1−t)2dt
We can rewrite the integrand as: (1+t)4(1−t)2=(1+t)2(1+t)2(1−t)2=(1+t1−t)2(1+t)21
Let's use the substitution v=1+t1−t. To find dv, we differentiate v with respect to t using the quotient rule: dtdv=(1+t)2dtd(1−t)⋅(1+t)−(1−t)⋅dtd(1+t)
dtdv=(1+t)2(−1)(1+t)−(1−t)(1)
dtdv=(1+t)2−1−t−(1−t)
dtdv=(1+t)2−1−t−1+t
dtdv=(1+t)2−2
From this, we can express (1+t)2dt in terms of dv:
dt=−2(1+t)2dv
(1+t)2dt=−21dv
Substitute v=1+t1−t and (1+t)2dt=−21dv into the integral:
I=∫(1+t1−t)2(1+t)21dt
I=∫v2(−21dv)
I=−21∫v2dv
Now, integrate with respect to v using the power rule ∫vndv=n+1vn+1+C:
I=−21(2+1v2+1)+C
I=−21(3v3)+C
I=−61v3+C
Finally, substitute back v=1+t1−t:
I=−61(1+t1−t)3+C
I=−6(1+t)3(1−t)3+C
This is the indefinite integral of the given function.
