Question
Question: $\int \frac{1 dx}{sin(x-a)sin(x-b)}$...
∫sin(x−a)sin(x−b)1dx
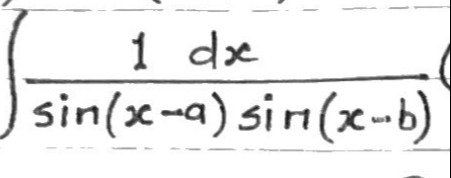
sin(b−a)1lnsin(x−a)sin(x−b)+C
Solution
To solve the integral ∫sin(x−a)sin(x−b)1dx, we use a standard technique for integrals of this form.
Let the integral be I. I=∫sin(x−a)sin(x−b)1dx We multiply the numerator and the denominator by sin(b−a), where b−a is the difference between the two angles in the denominator. This is a constant provided b=a+kπ for any integer k.
I=sin(b−a)1∫sin(x−a)sin(x−b)sin(b−a)dx We can rewrite the constant difference b−a as the difference of the angles in the denominator: (x−a)−(x−b)=x−a−x+b=b−a. So, we substitute sin(b−a)=sin((x−a)−(x−b)) in the numerator.
I=sin(b−a)1∫sin(x−a)sin(x−b)sin((x−a)−(x−b))dx Now, we use the trigonometric identity for the sine of a difference: sin(A−B)=sinAcosB−cosAsinB. Here, A=x−a and B=x−b. sin((x−a)−(x−b))=sin(x−a)cos(x−b)−cos(x−a)sin(x−b) Substitute this back into the integral: I=sin(b−a)1∫sin(x−a)sin(x−b)sin(x−a)cos(x−b)−cos(x−a)sin(x−b)dx Now, split the integrand into two separate fractions: I=sin(b−a)1∫(sin(x−a)sin(x−b)sin(x−a)cos(x−b)−sin(x−a)sin(x−b)cos(x−a)sin(x−b))dx Simplify each term: I=sin(b−a)1∫(sin(x−b)cos(x−b)−sin(x−a)cos(x−a))dx This simplifies to: I=sin(b−a)1∫(cot(x−b)−cot(x−a))dx We know that the integral of cot(u) with respect to u is ln∣sin(u)∣. Applying this: ∫cot(x−b)dx=ln∣sin(x−b)∣ ∫cot(x−a)dx=ln∣sin(x−a)∣ So, the integral becomes: I=sin(b−a)1(ln∣sin(x−b)∣−ln∣sin(x−a)∣)+C Using the logarithm property lnA−lnB=ln(A/B): I=sin(b−a)1lnsin(x−a)sin(x−b)+C This solution is valid provided sin(b−a)=0, which means b−a=kπ for any integer k.
Explanation of the solution:
- Multiply by sin(b−a): Introduce sin(b−a) in the numerator and denominator.
- Rewrite Numerator: Express sin(b−a) as sin((x−a)−(x−b)).
- Expand: Use sin(A−B)=sinAcosB−cosAsinB to expand the numerator.
- Split Fraction: Divide the numerator by the denominator sin(x−a)sin(x−b) to get two terms.
- Simplify: Cancel common factors to obtain cot(x−b)−cot(x−a).
- Integrate: Integrate each cotangent term: ∫cotudu=ln∣sinu∣.
- Combine: Combine the results using logarithm properties.
