Question

$\int \frac{1-7\cos^2x}{\sin^7x \cos x} dx$

Answer 1

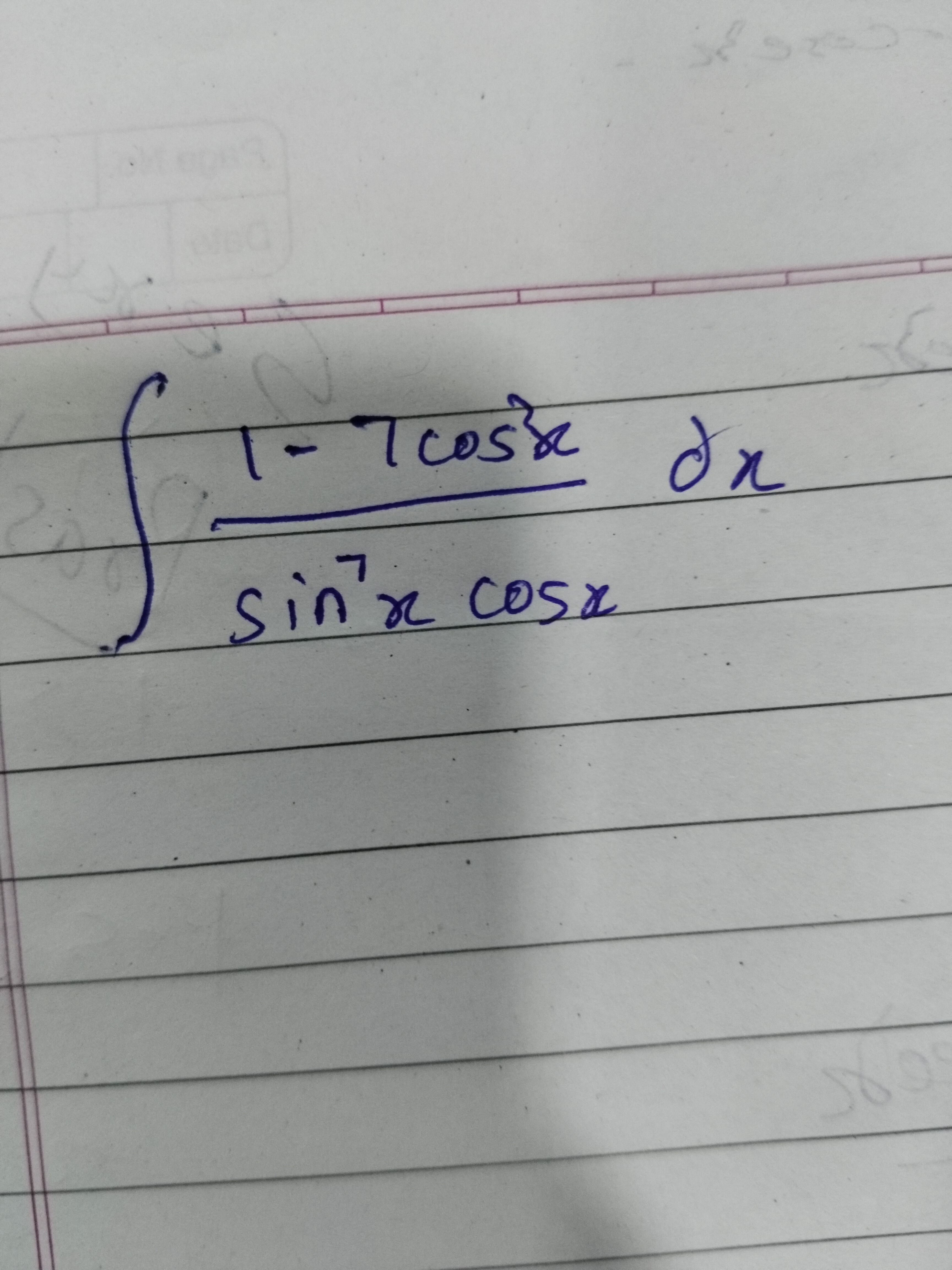
$\cot^6x + \frac{11}{4}\cot^4x + 2\cot^2x + \ln|\tan x| + C$

Answer 2

To solve the integral $\int \frac{1-7\cos^2x}{\sin^7x \cos x} dx$, we can use the substitution method by transforming the integrand into terms of $\tan x$ and $\sec^2 x$.

Step 1: Divide numerator and denominator by a suitable power of $\cos x$.

The highest power of $\sin x$ in the denominator is 7, and $\cos x$ is 1. The total power is 8. To convert the denominator to $\tan x$, we can divide by $\cos^8 x$.

$$\int \frac{\frac{1-7\cos^2x}{\cos^8x}}{\frac{\sin^7x \cos x}{\cos^8x}} dx = \int \frac{\frac{1}{\cos^8x} - \frac{7\cos^2x}{\cos^8x}}{\frac{\sin^7x}{\cos^7x}} dx$$ $$= \int \frac{\sec^8x - 7\sec^6x}{\tan^7x} dx$$

Step 2: Express $\sec x$ in terms of $\tan x$.

Recall the identity $\sec^2x = 1+\tan^2x$. So, $\sec^8x = (\sec^2x)^4 = (1+\tan^2x)^4$ and $\sec^6x = (\sec^2x)^3 = (1+\tan^2x)^3$. However, we need to save one $\sec^2x$ for $du$ when we substitute $u = \tan x$. Let's rewrite the numerator as: $\sec^8x - 7\sec^6x = \sec^6x (\sec^2x - 7) = (\sec^2x)^3 (\sec^2x - 7) = (1+\tan^2x)^3 (1+\tan^2x - 7)$ $= (1+\tan^2x)^3 (\tan^2x - 6)$. This is not quite right. We need $\sec^2x$ for $du$.

Let's factor out $\sec^2x$ from the numerator:

$$\int \frac{\sec^6x \cdot \sec^2x - 7\sec^4x \cdot \sec^2x}{\tan^7x} dx = \int \frac{\sec^2x [ \sec^6x - 7\sec^4x ]}{\tan^7x} dx$$

Now, express $\sec^6x$ and $\sec^4x$ in terms of $\tan x$: $\sec^6x = (\sec^2x)^3 = (1+\tan^2x)^3$ $\sec^4x = (\sec^2x)^2 = (1+\tan^2x)^2$

Substitute these into the integral:

$$\int \frac{[(1+\tan^2x)^3 - 7(1+\tan^2x)^2] \sec^2x}{\tan^7x} dx$$

Step 3: Perform $u$-substitution.

Let $u = \tan x$. Then $du = \sec^2x dx$. The integral becomes:

$$\int \frac{(1+u^2)^3 - 7(1+u^2)^2}{u^7} du$$

Step 4: Simplify the integrand in terms of $u$.

Factor out $(1+u^2)^2$ from the numerator:

$$\int \frac{(1+u^2)^2 [(1+u^2) - 7]}{u^7} du$$ $$= \int \frac{(1+u^2)^2 (u^2 - 6)}{u^7} du$$

Expand $(1+u^2)^2$:

$$= \int \frac{(1 + 2u^2 + u^4)(u^2 - 6)}{u^7} du$$

Expand the numerator:

$$= \int \frac{u^2 - 6 + 2u^4 - 12u^2 + u^6 - 6u^4}{u^7} du$$

Combine like terms in the numerator:

$$= \int \frac{u^6 + (2-6)u^4 + (1-12)u^2 - 6}{u^7} du$$ $$= \int \frac{u^6 - 4u^4 - 11u^2 - 6}{u^7} du$$

Divide each term by $u^7$:

$$= \int \left( \frac{u^6}{u^7} - \frac{4u^4}{u^7} - \frac{11u^2}{u^7} - \frac{6}{u^7} \right) du$$ $$= \int \left( u^{-1} - 4u^{-3} - 11u^{-5} - 6u^{-7} \right) du$$

Step 5: Integrate term by term.

$$= \ln|u| - 4\frac{u^{-2}}{-2} - 11\frac{u^{-4}}{-4} - 6\frac{u^{-6}}{-6} + C$$ $$= \ln|u| + 2u^{-2} + \frac{11}{4}u^{-4} + u^{-6} + C$$

Rewrite with positive exponents:

$$= \ln|u| + \frac{2}{u^2} + \frac{11}{4u^4} + \frac{1}{u^6} + C$$

Step 6: Substitute back $u = \tan x$.

$$= \ln|\tan x| + \frac{2}{\tan^2x} + \frac{11}{4\tan^4x} + \frac{1}{\tan^6x} + C$$

Using $\frac{1}{\tan x} = \cot x$:

$$= \cot^6x + \frac{11}{4}\cot^4x + 2\cot^2x + \ln|\tan x| + C$$

The final answer is $\boxed{\cot^6x + \frac{11}{4}\cot^4x + 2\cot^2x + \ln|\tan x| + C}$.

Explanation of the solution:

The integral is transformed by dividing the numerator and denominator by $\cos^8x$ to express it in terms of $\tan x$ and $\sec^2x$. A substitution $u = \tan x$ is then used, which simplifies the integrand into a polynomial in $u^{-1}$. This polynomial is then integrated term by term using the power rule for integration. Finally, the result is converted back to terms of $\tan x$ and $\cot x$.