Question
Question: $\int e^x(\frac{x^4+x^3-3x^2+x-2}{(x-1)^2})dx=e^x(\frac{f(x)}{x-1})+C$ then $f(2)$ is equal to ($f(x...
∫ex((x−1)2x4+x3−3x2+x−2)dx=ex(x−1f(x))+C then f(2) is equal to (f(x) is a polynomial)
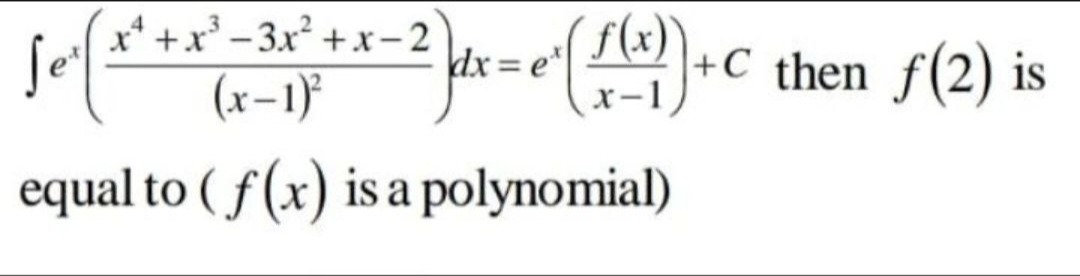
7
8
9
10
9
Solution
The integral is of the form ∫exG(x)dx=exH(x)+C, where G(x)=(x−1)2x4+x3−3x2+x−2 and H(x)=x−1f(x). This implies G(x)=H(x)+H′(x). We can decompose G(x) using polynomial long division or substitution. Let u=x−1, so x=u+1. G(x)=u2(u+1)4+(u+1)3−3(u+1)2+(u+1)−2 G(x)=u2u4+5u3+6u2+2u−2=u2+5u+6+u22u−2 Substituting back u=x−1: G(x)=(x−1)2+5(x−1)+6+(x−1)22(x−1)−2 G(x)=(x2−2x+1)+(5x−5)+6+(x−1)22x−4 G(x)=x2+3x+2+(x−1)22x−4 We need to find H(x) such that H(x)+H′(x)=G(x). Let H(x)=P(x)+x−1K, where P(x) is a polynomial. Then H′(x)=P′(x)−(x−1)2K. H(x)+H′(x)=P(x)+P′(x)+x−1K−(x−1)2K. Comparing with G(x)=x2+3x+2+(x−1)22x−4: P(x)+P′(x)=x2+3x+2. If P(x)=x2+x+1, then P′(x)=2x+1, and P(x)+P′(x)=x2+3x+2. x−1K−(x−1)2K=(x−1)22x−4. Multiplying by (x−1)2, we get K(x−1)−K=2x−4, which simplifies to Kx−2K=2x−4. Thus, K=2. So, H(x)=x2+x+1+x−12. Given H(x)=x−1f(x): x−1f(x)=x2+x+1+x−12=x−1(x2+x+1)(x−1)+2 f(x)=(x2+x+1)(x−1)+2=(x3−1)+2=x3+1. We need to find f(2): f(2)=(2)3+1=8+1=9.
