Solveeit Logo
Login

Question

Question: $\int e^x \left[ \frac{x-3}{(x-1)^3} \right] dx$...

∫ex[x−3(x−1)3]dx\int e^x \left[ \frac{x-3}{(x-1)^3} \right] dx

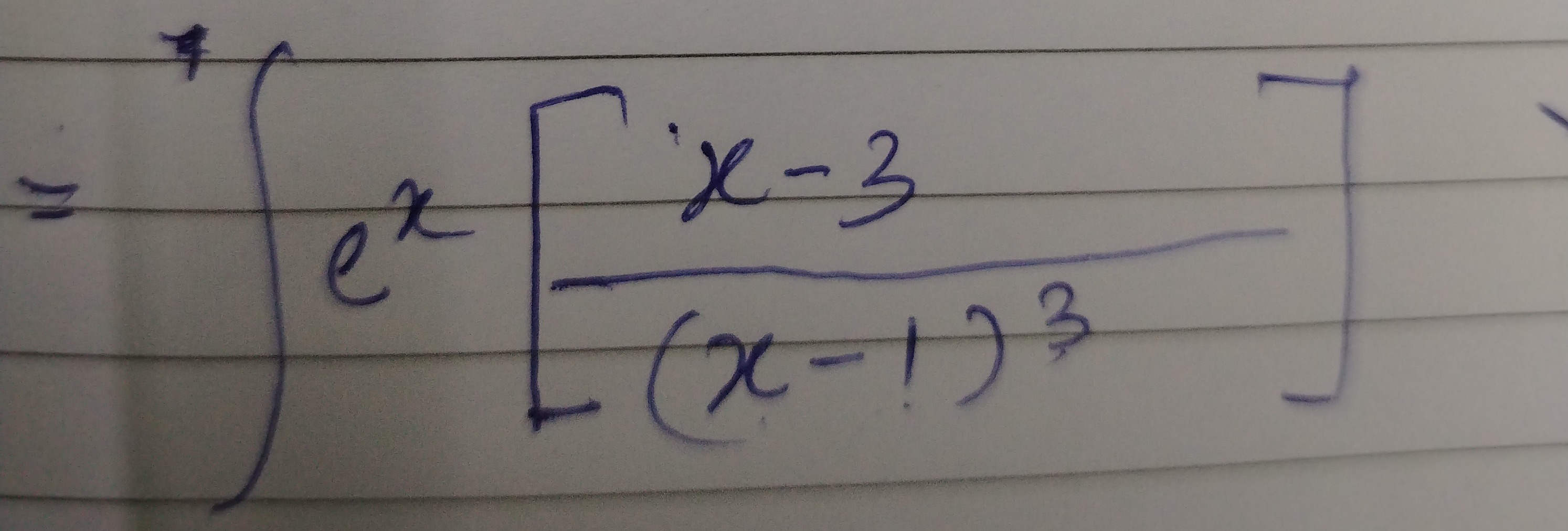
Answer

ex(x−1)2+C\frac{e^x}{(x-1)^2} + C

Explanation

Solution

The integral ∫ex[x−3(x−1)3]dx\int e^x \left[ \frac{x-3}{(x-1)^3} \right] dx is evaluated by recognizing the form ∫ex[f(x)+f′(x)]dx=exf(x)+C\int e^x [f(x) + f'(x)] dx = e^x f(x) + C.

  1. Rewrite the numerator x−3x-3 as (x−1)−2(x-1)-2.
  2. Split the fraction: (x−1)−2(x−1)3=x−1(x−1)3−2(x−1)3=1(x−1)2−2(x−1)3\frac{(x-1)-2}{(x-1)^3} = \frac{x-1}{(x-1)^3} - \frac{2}{(x-1)^3} = \frac{1}{(x-1)^2} - \frac{2}{(x-1)^3}.
  3. Identify f(x)=1(x−1)2f(x) = \frac{1}{(x-1)^2}.
  4. Calculate f′(x)f'(x): f′(x)=ddx((x−1)−2)=−2(x−1)−3=−2(x−1)3f'(x) = \frac{d}{dx}((x-1)^{-2}) = -2(x-1)^{-3} = -\frac{2}{(x-1)^3}.
  5. The integrand is now in the form ex[f(x)+f′(x)]e^x [f(x) + f'(x)].
  6. Apply the formula: ∫ex[f(x)+f′(x)]dx=exf(x)+C=ex⋅1(x−1)2+C\int e^x [f(x) + f'(x)] dx = e^x f(x) + C = e^x \cdot \frac{1}{(x-1)^2} + C.