Question

$\int e^{3x-2} dx$

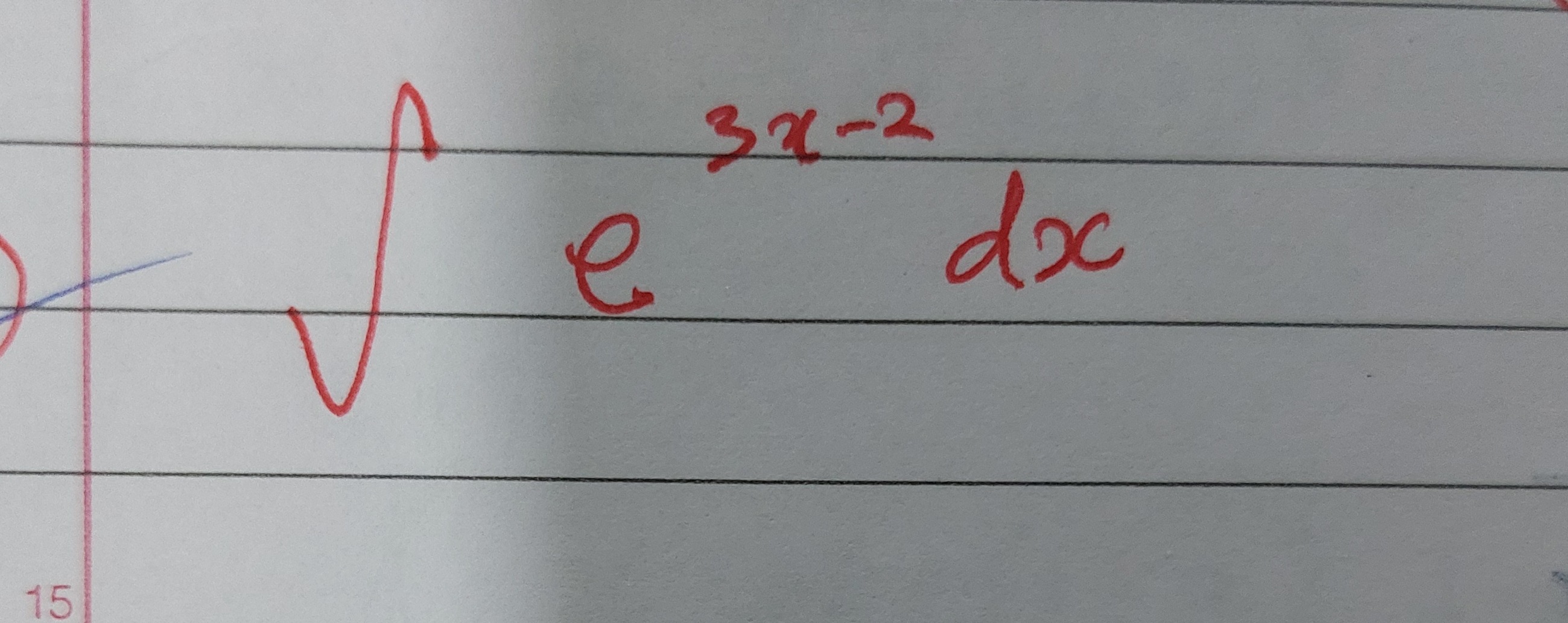
Answer 1

$\frac{1}{3}e^{3x-2} + C$

Answer 2

Solution:

Let

$$u = 3x - 2 \quad \Rightarrow \quad \frac{du}{dx} = 3 \quad \Rightarrow \quad dx = \frac{du}{3}.$$

Substitute into the integral:

$$\int e^{3x-2} dx = \int e^{u} \frac{du}{3} = \frac{1}{3}\int e^u \, du = \frac{1}{3}e^u + C.$$

Replace $u$ with $3x-2$:

$$\frac{1}{3}e^{3x-2} + C.$$

---

Minimal Explanation:
Substitute $u=3x-2$ so that $dx=\frac{du}{3}$. The integral becomes $\frac{1}{3}\int e^u\,du = \frac{1}{3}e^u + C$. Substitute back.