Question
Question: $\int dx \frac{1+z^x}{1-_{9}x}$...
∫dx1−9x1+zx
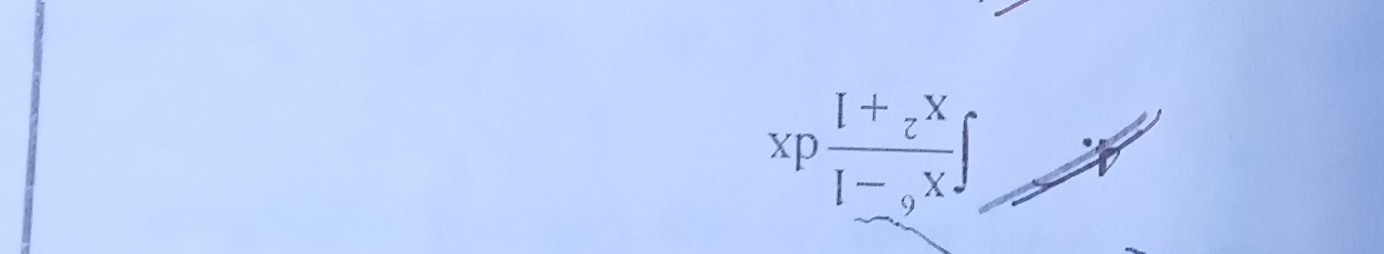
Answer
∫1−9x1+zxdx=−91ln∣1−9x∣+9z1/9Ei(−9lnz(1−9x))+C.
Explanation
Solution
-
Split the integral into two parts.
-
In the first, substitute u=1−9x to integrate ∫1−9xdx.
-
In the second, write zx=exlnz and use the same substitution; recognize the definition of the exponential integral Ei(−Au).
-
Combine the answers.
