Question

$\int cos(3x+4) dx$

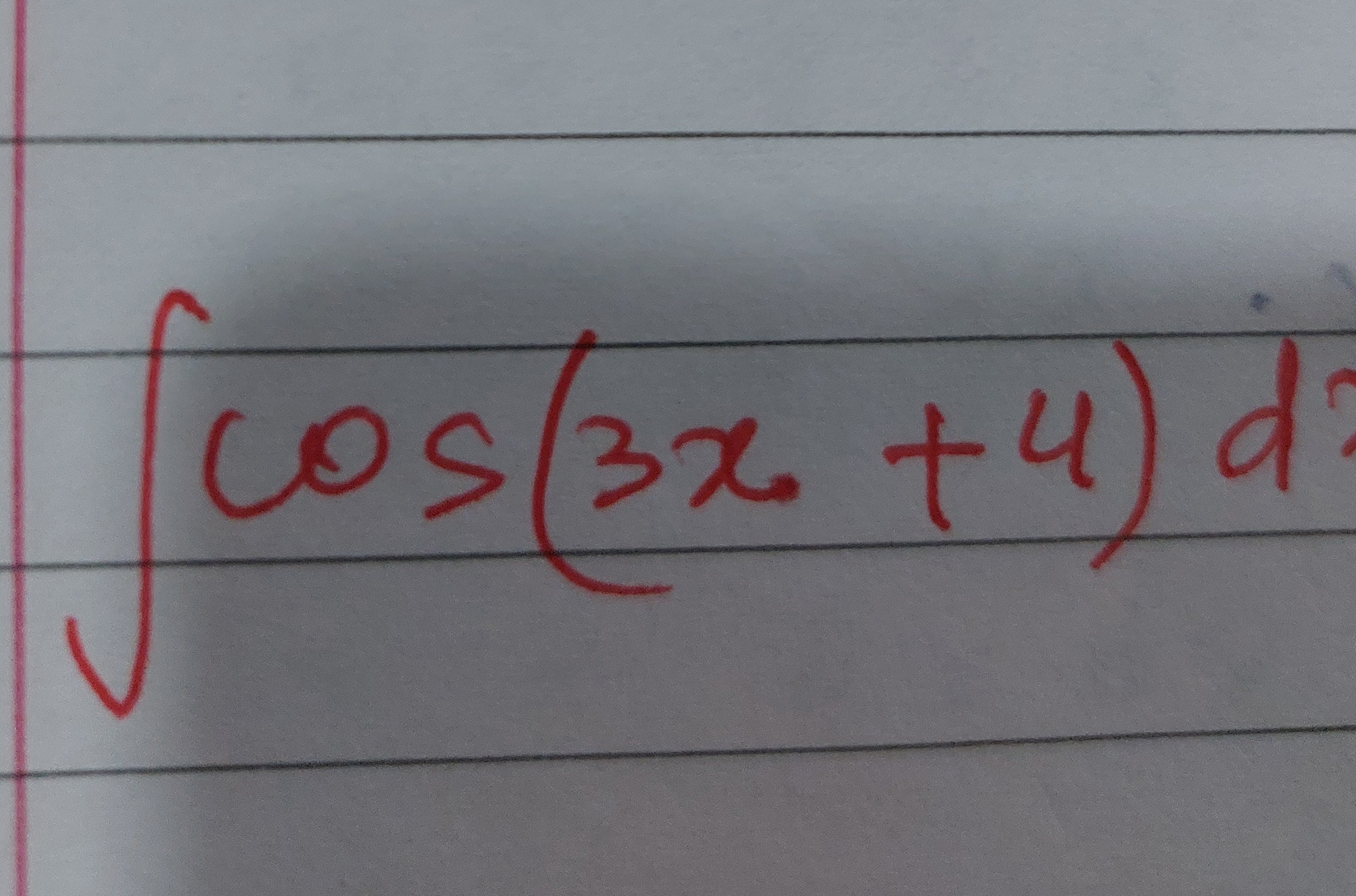
Answer 1

$\frac{1}{3}\sin(3x+4) + C$

Answer 2

Step 1: Let $u = 3x+4$. Then, $\frac{du}{dx} = 3$ which gives $dx = \frac{du}{3}$.

Step 2: Substitute into the integral:

$$\int \cos(3x+4) \, dx = \int \cos(u) \frac{du}{3} = \frac{1}{3}\int \cos(u) \, du$$

Step 3: Integrate:

$$\frac{1}{3}\int \cos(u) \, du = \frac{1}{3}\sin(u) + C$$

Step 4: Substitute back $u = 3x+4$:

$$\frac{1}{3}\sin(3x+4) + C$$

---

Explanation (minimal): Substitute $u = 3x+4$; integrate $\cos(u)$ to get $\sin(u)$; revert substitution.