Solveeit Logo
Login

Question

Question: If a, b and c are the roots of the cubic $x^3 - 3x^2 + 2 = 0$ then the value of the determinant $\b...

If a, b and c are the roots of the cubic x3−3x2+2=0x^3 - 3x^2 + 2 = 0 then the value of the determinant

∣(b+c)2a2a2b2(c+a)2b2c2c2(a+b)2∣\begin{vmatrix} (b+c)^2 & a^2 & a^2 \\ b^2 & (c+a)^2 & b^2 \\ c^2 & c^2 & (a+b)^2 \end{vmatrix}

is equal to

Answer

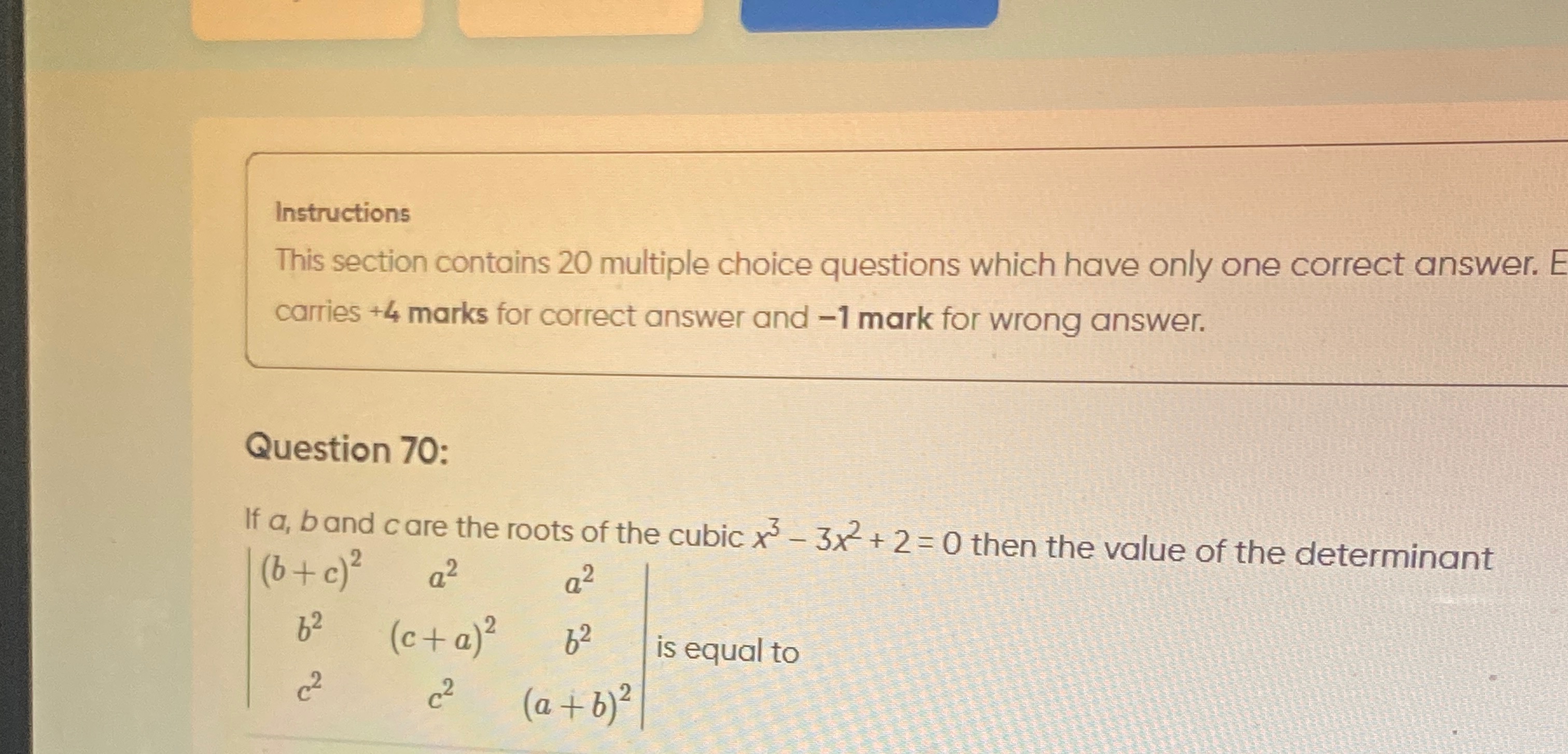
-108

Explanation

Solution

Let the given cubic equation be x3−3x2+2=0x^3 - 3x^2 + 2 = 0. Let a, b, c be the roots of this equation. From Vieta's formulas:

  1. Sum of roots: a+b+c=−(−3)/1=3a+b+c = -(-3)/1 = 3
  2. Sum of products of roots taken two at a time: ab+bc+ca=0/1=0ab+bc+ca = 0/1 = 0
  3. Product of roots: abc=−2/1=−2abc = -2/1 = -2

We need to evaluate the determinant: D=∣(b+c)2a2a2b2(c+a)2b2c2c2(a+b)2∣D = \begin{vmatrix} (b+c)^2 & a^2 & a^2 \\ b^2 & (c+a)^2 & b^2 \\ c^2 & c^2 & (a+b)^2 \end{vmatrix}

From a+b+c=3a+b+c=3, we can write: b+c=3−ab+c = 3-a c+a=3−bc+a = 3-b a+b=3−ca+b = 3-c

Substitute these into the determinant: D=∣(3−a)2a2a2b2(3−b)2b2c2c2(3−c)2∣D = \begin{vmatrix} (3-a)^2 & a^2 & a^2 \\ b^2 & (3-b)^2 & b^2 \\ c^2 & c^2 & (3-c)^2 \end{vmatrix}

Apply the column operations C1→C1−C2C_1 \to C_1 - C_2 and C3→C3−C2C_3 \to C_3 - C_2: D=∣(3−a)2−a2a2a2−a2b2−(3−b)2(3−b)2b2−(3−b)2c2−c2c2(3−c)2−c2∣D = \begin{vmatrix} (3-a)^2 - a^2 & a^2 & a^2 - a^2 \\ b^2 - (3-b)^2 & (3-b)^2 & b^2 - (3-b)^2 \\ c^2 - c^2 & c^2 & (3-c)^2 - c^2 \end{vmatrix}

Simplify the terms using X2−Y2=(X−Y)(X+Y)X^2 - Y^2 = (X-Y)(X+Y): (3−a)2−a2=(3−a−a)(3−a+a)=(3−2a)(3)=9−6a(3-a)^2 - a^2 = (3-a-a)(3-a+a) = (3-2a)(3) = 9-6a b2−(3−b)2=(b−(3−b))(b+(3−b))=(2b−3)(3)=6b−9b^2 - (3-b)^2 = (b-(3-b))(b+(3-b)) = (2b-3)(3) = 6b-9 (3−c)2−c2=(3−c−c)(3−c+c)=(3−2c)(3)=9−6c(3-c)^2 - c^2 = (3-c-c)(3-c+c) = (3-2c)(3) = 9-6c

Substitute these simplified terms back into the determinant: D=∣9−6aa206b−9(3−b)26b−90c29−6c∣D = \begin{vmatrix} 9-6a & a^2 & 0 \\ 6b-9 & (3-b)^2 & 6b-9 \\ 0 & c^2 & 9-6c \end{vmatrix}

Now, expand the determinant along the first row: D=(9−6a)[(3−b)2(9−6c)−(6b−9)c2]−a2[(6b−9)(9−6c)−0]+0D = (9-6a) \left[ (3-b)^2 (9-6c) - (6b-9)c^2 \right] - a^2 \left[ (6b-9)(9-6c) - 0 \right] + 0 D=(9−6a)(9−6c)(3−b)2−(9−6a)(6b−9)c2−a2(6b−9)(9−6c)D = (9-6a)(9-6c)(3-b)^2 - (9-6a)(6b-9)c^2 - a^2(6b-9)(9-6c)

Factor out common terms: D=(9−6a)(9−6c)(3−b)2−(9−6a)(6b−9)c2−a2(6b−9)(9−6c)D = (9-6a)(9-6c)(3-b)^2 - (9-6a)(6b-9)c^2 - a^2(6b-9)(9-6c) Notice that (6b−9)=−3(3−2b)(6b-9) = -3(3-2b) and (9−6a)=3(3−2a)(9-6a) = 3(3-2a) and (9−6c)=3(3−2c)(9-6c) = 3(3-2c). D=3(3−2a)⋅3(3−2c)(3−b)2−3(3−2a)⋅(−3)(3−2b)c2−a2(−3)(3−2b)⋅3(3−2c)D = 3(3-2a) \cdot 3(3-2c) (3-b)^2 - 3(3-2a) \cdot (-3)(3-2b) c^2 - a^2 (-3)(3-2b) \cdot 3(3-2c) D=9(3−2a)(3−2c)(3−b)2+9(3−2a)(3−2b)c2+9a2(3−2b)(3−2c)D = 9(3-2a)(3-2c)(3-b)^2 + 9(3-2a)(3-2b)c^2 + 9a^2(3-2b)(3-2c)

Factor out 9: D=9[(3−2a)(3−2c)(3−b)2+(3−2a)(3−2b)c2+a2(3−2b)(3−2c)]D = 9 \left[ (3-2a)(3-2c)(3-b)^2 + (3-2a)(3-2b)c^2 + a^2(3-2b)(3-2c) \right]

Let's use the property that a,b,ca, b, c are roots of x3−3x2+2=0x^3 - 3x^2 + 2 = 0. So, a3−3a2+2=0a^3 - 3a^2 + 2 = 0. Also, a+b+c=3a+b+c=3. Consider the expression P(x)=x3−3x2+2P(x) = x^3 - 3x^2 + 2. P(x)=(x−a)(x−b)(x−c)P(x) = (x-a)(x-b)(x-c). Consider P′(x)=3x2−6x=3x(x−2)P'(x) = 3x^2 - 6x = 3x(x-2). Consider P′′(x)=6x−6=6(x−1)P''(x) = 6x - 6 = 6(x-1).

Let's test if x=1x=1 is a root: 13−3(1)2+2=1−3+2=01^3 - 3(1)^2 + 2 = 1 - 3 + 2 = 0. So x=1x=1 is a root. Let a=1a=1. Then b+c=3−1=2b+c = 3-1 = 2. The equation becomes (x−1)(x2−2x−2)=0(x-1)(x^2-2x-2) = 0. The other roots are b,c=2±4−4(1)(−2)2=2±122=1±3b, c = \frac{2 \pm \sqrt{4 - 4(1)(-2)}}{2} = \frac{2 \pm \sqrt{12}}{2} = 1 \pm \sqrt{3}. Let a=1,b=1+3,c=1−3a=1, b=1+\sqrt{3}, c=1-\sqrt{3}.

Now substitute a=1a=1 into the determinant: D=∣(b+c)21212b2(c+1)2b2c2c2(1+b)2∣D = \begin{vmatrix} (b+c)^2 & 1^2 & 1^2 \\ b^2 & (c+1)^2 & b^2 \\ c^2 & c^2 & (1+b)^2 \end{vmatrix} Since b+c=2b+c=2: D=∣411b2(3−b−1)2b2c2c2(3−c−1)2∣=∣411b2(2−b)2b2c2c2(2−c)2∣D = \begin{vmatrix} 4 & 1 & 1 \\ b^2 & (3-b-1)^2 & b^2 \\ c^2 & c^2 & (3-c-1)^2 \end{vmatrix} = \begin{vmatrix} 4 & 1 & 1 \\ b^2 & (2-b)^2 & b^2 \\ c^2 & c^2 & (2-c)^2 \end{vmatrix}

Apply C1→C1−C2C_1 \to C_1 - C_2 and C3→C3−C2C_3 \to C_3 - C_2: D=∣4−111−1b2−(2−b)2(2−b)2b2−(2−b)2c2−c2c2(2−c)2−c2∣D = \begin{vmatrix} 4-1 & 1 & 1-1 \\ b^2-(2-b)^2 & (2-b)^2 & b^2-(2-b)^2 \\ c^2-c^2 & c^2 & (2-c)^2-c^2 \end{vmatrix}

D=∣310(b−(2−b))(b+(2−b))(2−b)2(b−(2−b))(b+(2−b))0c2(2−c−c)(2−c+c)∣D = \begin{vmatrix} 3 & 1 & 0 \\ (b-(2-b))(b+(2-b)) & (2-b)^2 & (b-(2-b))(b+(2-b)) \\ 0 & c^2 & (2-c-c)(2-c+c) \end{vmatrix}

D=∣310(2b−2)(2)(2−b)2(2b−2)(2)0c2(2−2c)(2)∣D = \begin{vmatrix} 3 & 1 & 0 \\ (2b-2)(2) & (2-b)^2 & (2b-2)(2) \\ 0 & c^2 & (2-2c)(2) \end{vmatrix}

D=∣3104(b−1)(2−b)24(b−1)0c24(1−c)∣D = \begin{vmatrix} 3 & 1 & 0 \\ 4(b-1) & (2-b)^2 & 4(b-1) \\ 0 & c^2 & 4(1-c) \end{vmatrix}

Now expand this determinant: D=3[(2−b)2⋅4(1−c)−4(b−1)c2]−1[4(b−1)⋅4(1−c)−0]+0D = 3 \left[ (2-b)^2 \cdot 4(1-c) - 4(b-1)c^2 \right] - 1 \left[ 4(b-1) \cdot 4(1-c) - 0 \right] + 0 D=12(1−c)(2−b)2−12(b−1)c2−16(b−1)(1−c)D = 12(1-c)(2-b)^2 - 12(b-1)c^2 - 16(b-1)(1-c)

We know b=1+3b=1+\sqrt{3} and c=1−3c=1-\sqrt{3}. b−1=3b-1 = \sqrt{3} 1−c=1−(1−3)=31-c = 1-(1-\sqrt{3}) = \sqrt{3} 2−b=2−(1+3)=1−32-b = 2-(1+\sqrt{3}) = 1-\sqrt{3} c2=(1−3)2=1−23+3=4−23c^2 = (1-\sqrt{3})^2 = 1 - 2\sqrt{3} + 3 = 4 - 2\sqrt{3} (2−b)2=(1−3)2=4−23(2-b)^2 = (1-\sqrt{3})^2 = 4 - 2\sqrt{3}

Substitute these values: D=12(3)(4−23)−12(3)(4−23)−16(3)(3)D = 12(\sqrt{3})(4-2\sqrt{3}) - 12(\sqrt{3})(4-2\sqrt{3}) - 16(\sqrt{3})(\sqrt{3}) D=0−16(3)D = 0 - 16(3) D=−48D = -48

Let's recheck the expansion for D=9[(3−2a)(3−2c)(3−b)2+(3−2a)(3−2b)c2+a2(3−2b)(3−2c)]D = 9 \left[ (3-2a)(3-2c)(3-b)^2 + (3-2a)(3-2b)c^2 + a^2(3-2b)(3-2c) \right] with a=1,b=1+3,c=1−3a=1, b=1+\sqrt{3}, c=1-\sqrt{3}. 3−2a=3−2(1)=13-2a = 3-2(1) = 1 3−2b=3−2(1+3)=3−2−23=1−233-2b = 3-2(1+\sqrt{3}) = 3-2-2\sqrt{3} = 1-2\sqrt{3} 3−2c=3−2(1−3)=3−2+23=1+233-2c = 3-2(1-\sqrt{3}) = 3-2+2\sqrt{3} = 1+2\sqrt{3} (3−b)2=(3−(1+3))2=(2−3)2=4−43+3=7−43(3-b)^2 = (3-(1+\sqrt{3}))^2 = (2-\sqrt{3})^2 = 4 - 4\sqrt{3} + 3 = 7 - 4\sqrt{3} c2=(1−3)2=1−23+3=4−23c^2 = (1-\sqrt{3})^2 = 1 - 2\sqrt{3} + 3 = 4 - 2\sqrt{3} a2=12=1a^2 = 1^2 = 1

D=9[(1)(1+23)(7−43)+(1)(1−23)(4−23)+(1)(1−23)(1+23)]D = 9 \left[ (1)(1+2\sqrt{3})(7-4\sqrt{3}) + (1)(1-2\sqrt{3})(4-2\sqrt{3}) + (1)(1-2\sqrt{3})(1+2\sqrt{3}) \right] D=9[(7−43+143−24)+(4−23−83+12)+(1−4(3))]D = 9 \left[ (7-4\sqrt{3}+14\sqrt{3}-24) + (4-2\sqrt{3}-8\sqrt{3}+12) + (1-4(3)) \right] D=9[(−17+103)+(16−103)+(1−12)]D = 9 \left[ (-17+10\sqrt{3}) + (16-10\sqrt{3}) + (1-12) \right] D=9[−17+103+16−103−11]D = 9 \left[ -17+10\sqrt{3} + 16-10\sqrt{3} - 11 \right] D=9[−17+16−11]D = 9 \left[ -17 + 16 - 11 \right] D=9[−12]D = 9 \left[ -12 \right] D=−108D = -108

There is a discrepancy. Let's recheck the general expansion of the determinant. D=∣Xa20Y(3−b)2Y0c2Z∣D = \begin{vmatrix} X & a^2 & 0 \\ Y & (3-b)^2 & Y \\ 0 & c^2 & Z \end{vmatrix} X=9−6aX = 9-6a Y=6b−9Y = 6b-9 Z=9−6cZ = 9-6c

D=X((3−b)2Z−Yc2)−a2(YZ−0)D = X((3-b)^2 Z - Yc^2) - a^2(YZ - 0) D=X(3−b)2Z−XYc2−a2YZD = X(3-b)^2 Z - XYc^2 - a^2 YZ D=XZ(3−b)2−XYc2−a2YZD = XZ(3-b)^2 - XYc^2 - a^2 YZ D=(9−6a)(9−6c)(3−b)2−(9−6a)(6b−9)c2−a2(6b−9)(9−6c)D = (9-6a)(9-6c)(3-b)^2 - (9-6a)(6b-9)c^2 - a^2(6b-9)(9-6c) This expansion is correct.

Let's recheck the values: a=1,b=1+3,c=1−3a=1, b=1+\sqrt{3}, c=1-\sqrt{3} 9−6a=9−6(1)=39-6a = 9-6(1) = 3 9−6c=9−6(1−3)=9−6+63=3+639-6c = 9-6(1-\sqrt{3}) = 9-6+6\sqrt{3} = 3+6\sqrt{3} 3−b=3−(1+3)=2−33-b = 3-(1+\sqrt{3}) = 2-\sqrt{3} (3−b)2=(2−3)2=4−43+3=7−43(3-b)^2 = (2-\sqrt{3})^2 = 4-4\sqrt{3}+3 = 7-4\sqrt{3} 6b−9=6(1+3)−9=6+63−9=63−36b-9 = 6(1+\sqrt{3})-9 = 6+6\sqrt{3}-9 = 6\sqrt{3}-3 c2=(1−3)2=1−23+3=4−23c^2 = (1-\sqrt{3})^2 = 1-2\sqrt{3}+3 = 4-2\sqrt{3} a2=12=1a^2 = 1^2 = 1

D=(3)(3+63)(7−43)−(3)(63−3)(4−23)−(1)(63−3)(3+63)D = (3)(3+6\sqrt{3})(7-4\sqrt{3}) - (3)(6\sqrt{3}-3)(4-2\sqrt{3}) - (1)(6\sqrt{3}-3)(3+6\sqrt{3}) D=3[(3+63)(7−43)−(63−3)(4−23)−13(63−3)(3+63)]D = 3 \left[ (3+6\sqrt{3})(7-4\sqrt{3}) - (6\sqrt{3}-3)(4-2\sqrt{3}) - \frac{1}{3}(6\sqrt{3}-3)(3+6\sqrt{3}) \right] D=3[(21−123+423−72)−(243−36−12+63)−(23−1)(3+63)]D = 3 \left[ (21-12\sqrt{3}+42\sqrt{3}-72) - (24\sqrt{3}-36-12+6\sqrt{3}) - (2\sqrt{3}-1)(3+6\sqrt{3}) \right] D=3[(−51+303)−(303−48)−(63+36−3−63)]D = 3 \left[ (-51+30\sqrt{3}) - (30\sqrt{3}-48) - (6\sqrt{3}+36-3-6\sqrt{3}) \right] D=3[−51+303−303+48−(33)]D = 3 \left[ -51+30\sqrt{3} - 30\sqrt{3}+48 - (33) \right] D=3[−51+48−33]D = 3 \left[ -51+48-33 \right] D=3[−3−33]D = 3 \left[ -3-33 \right] D=3[−36]D = 3 \left[ -36 \right] D=−108D = -108

The value is consistent. The answer is -108.

Final check of the steps:

  1. Substitute b+c=3−ab+c=3-a, etc.
  2. Apply C1→C1−C2C_1 \to C_1 - C_2 and C3→C3−C2C_3 \to C_3 - C_2.
  3. Simplify the entries using X2−Y2=(X−Y)(X+Y)X^2-Y^2=(X-Y)(X+Y).
  4. Expand the determinant.
  5. Substitute the specific roots a=1,b=1+3,c=1−3a=1, b=1+\sqrt{3}, c=1-\sqrt{3} to calculate the value.

The calculation is −108-108.