Question

If the matrix $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ satisfies the matrix equation $X^2 - (a+d)X + kI = 0$, then (where I is identify matrix of order 2)

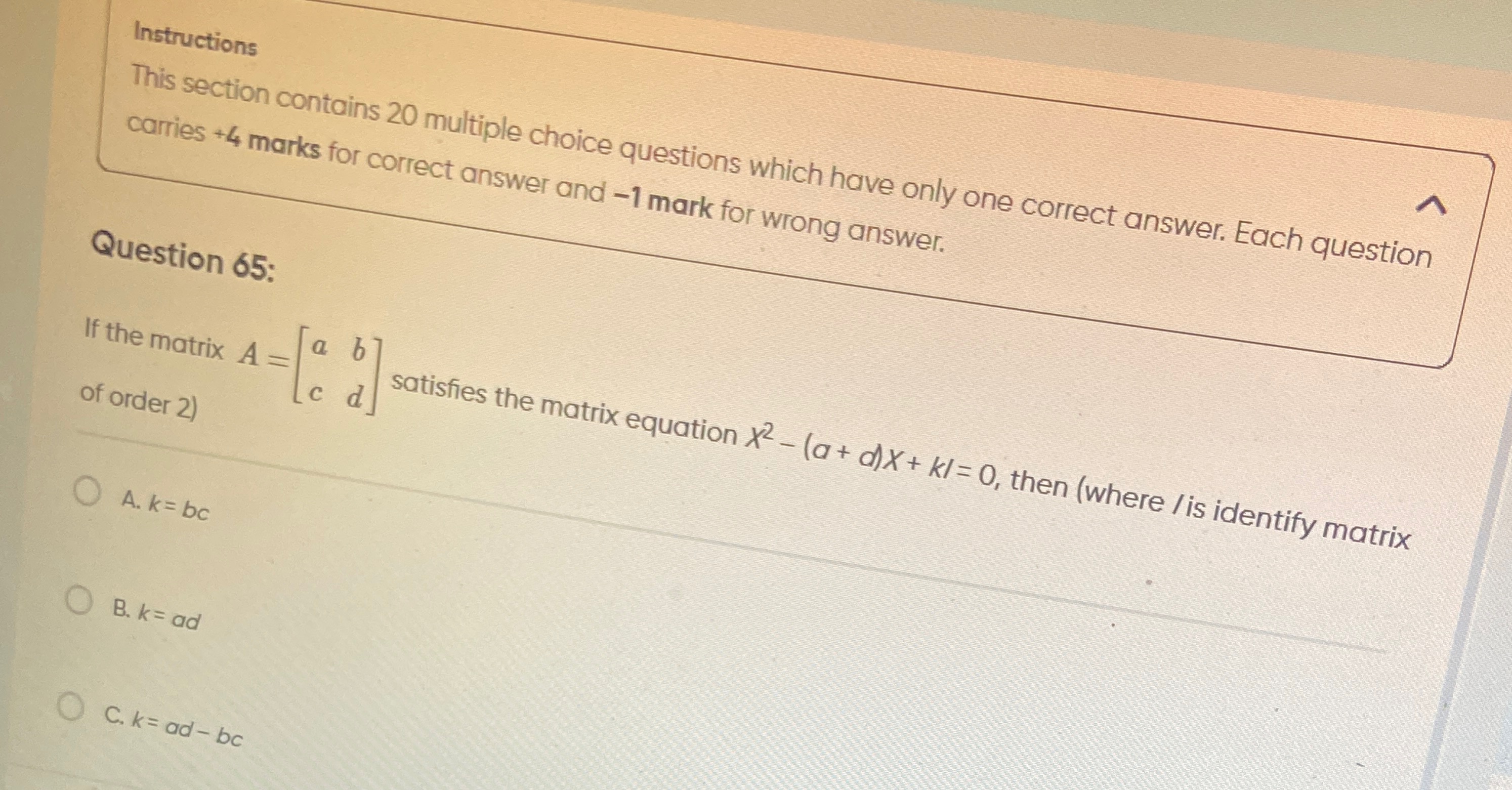
• A. k = bc
• B. k = ad
• C. k = ad - bc

Answer 1

Answer: (C)

k = ad - bc

Answer 2

The problem asks us to find the value of $k$ in the given matrix equation $X^2 - (a+d)X + kI = 0$, where $X = A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ and $I$ is the identity matrix of order 2.

This problem can be solved using the Cayley-Hamilton Theorem, which states that every square matrix satisfies its own characteristic equation.

1. Find the Characteristic Equation of Matrix A:

For a 2x2 matrix $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$, the characteristic equation is given by $\det(A - \lambda I) = 0$.

First, form the matrix $A - \lambda I$:

$$A - \lambda I = \begin{bmatrix} a & b \\ c & d \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} a-\lambda & b \\ c & d-\lambda \end{bmatrix}$$

Next, calculate the determinant:

$$\det(A - \lambda I) = (a-\lambda)(d-\lambda) - (b)(c) = 0$$ $$ad - a\lambda - d\lambda + \lambda^2 - bc = 0$$

Rearranging the terms in descending powers of $\lambda$:

$$\lambda^2 - (a+d)\lambda + (ad - bc) = 0$$

This is the characteristic equation of matrix A.

2. Apply the Cayley-Hamilton Theorem:

According to the Cayley-Hamilton Theorem, if a matrix A satisfies its characteristic equation, we can replace $\lambda$ with A, and the constant term with the constant multiplied by the identity matrix I. So, replacing $\lambda$ with A in the characteristic equation:

$$A^2 - (a+d)A + (ad - bc)I = 0$$

3. Compare with the Given Equation:

The problem states that the matrix A satisfies the equation $X^2 - (a+d)X + kI = 0$. Since X is A, we have:

$$A^2 - (a+d)A + kI = 0$$

Comparing this equation with the one derived from the Cayley-Hamilton Theorem:

$$A^2 - (a+d)A + (ad - bc)I = 0$$

By comparing the coefficients of the identity matrix, we can see that:

$$k = ad - bc$$

The value $a+d$ is the trace of the matrix A, and $ad-bc$ is the determinant of the matrix A. So, the characteristic equation for a 2x2 matrix A can be written as $\lambda^2 - \text{Tr}(A)\lambda + \text{Det}(A) = 0$, and by Cayley-Hamilton Theorem, $A^2 - \text{Tr}(A)A + \text{Det}(A)I = 0$. Thus, $k = \text{Det}(A)$.