Question

Instantaneous center of the rotation of disc is located at

$\begin{aligned} & A.\text{ }0.2m\text{ below o} \\\ & \text{B}\text{. 0}\text{.2 above o} \\\ & C.\text{ 0}\text{.6m above o} \\\ & \text{D}\text{. 0}\text{.4m below o} \\\ \end{aligned}$

Answer 1

Instantaneous center of rotation is the point where the velocity is zero at a particular point and particular time the point is fixed to a body. In order to find the solution for the above question we have to find the point where the velocity is zero at a particular instant of time.
Formula used:
$\Rightarrow v=r\omega$
$\to$ v = tangential velocity
$\to$ω = angular velocity
$\to$r = wheel radius or the disc radius

Complete answer:
Given data
Angular velocity (ω) = 10rad/s
Velocity (v) = 4m/s
Radius of the disc (r) = 0.2m

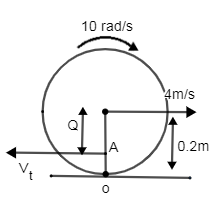
Now suppose A is the point where velocity is zero at instant of time as shown in the figure.
Let the center of mass of disc be C and the distance at point A from C is Q
Now tangential velocity at point A is
$\Rightarrow vt=Q\times \omega .....(1)$
Now velocity of the disc is
$\Rightarrow v=4m/s.....(2)$
Now in order to get the instantaneous center the velocity needs to be zero at a particular instant of time.
Hence,
$\Rightarrow vt-v=0...(3)$
Here put (-ve) sign because both are in opposite directions as shown in figure. Now substitute value of equation (1) and (2) in equation (3)
$\begin{aligned} & \Rightarrow Q\times \omega -4=0 \\\ & \Rightarrow Q\times 10=4 \\\ & \Rightarrow Q=\dfrac{4}{10} \\\ & \therefore Q=0.4m \\\ \end{aligned}$

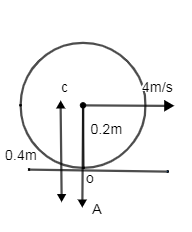
So instantaneous center of rotation is 0.4m from center of mass C. Hence distance from O is 0.2m

So that correct answer is option (A) 0.2m below O.

Note:
Here we are getting an answer as 0.4 m so we can be mistaken by thinking option (D) is correct but we have to notice that we find an instantaneous center from center of mass C which is 0.2 m above O so our correct answer will be 0.2 m below point O.