Question
Question: Inside a uniform sphere of mass $M$ and radius $R$, a cavity of Radius $\frac{R}{3}$ is made as show...
Inside a uniform sphere of mass M and radius R, a cavity of Radius 3R is made as shown in figure. Gravitational potential at the centre of sphere is:
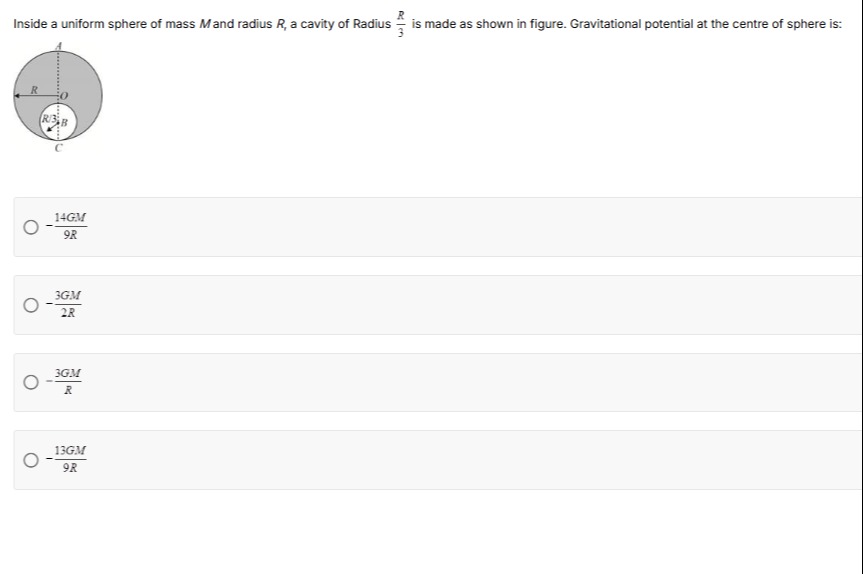
9R−14GM
2R−3GM
R−3GM
9R−13GM
9R−13GM
Solution
Solution:
-
Step 1. Treat the problem by superposition. A sphere of mass M and radius R has gravitational potential at its center
ϕfull=−2R3GM. -
Step 2. The cavity is removed. Removing a region is equivalent to adding a “negative mass” distribution. Its density is the same as the full sphere:
ρ=4πR33M.The mass removed (if the cavity were filled) is
mcav=ρ(34π(3R)3)=4πR33M⋅814πR3=27M.Thus we have a negative mass −mcav=−27M.
-
Step 3. It is given (from the figure) that the cavity is such that its surface touches the outer sphere. Hence the distance from the center of the full sphere (point O) to the center of the cavity (point B) is
OB=R−3R=32R.Since O lies outside the cavity, the potential due to the negative mass is the same as that of a point mass:
ϕcav=−OBG(−mcav)=−32RG(−27M)=27GM⋅2R3=18RGM. -
Step 4. The net potential at O is the sum:
ϕ(O)=ϕfull+ϕcav=−2R3GM+18RGMWriting with a common denominator:
−2R3GM=−18R27GM⟹ϕ(O)=−18R27GM+18RGM=−18R26GM=−9R13GM.
Thus, the gravitational potential at the center of the sphere is
9R−13GM.Core Explanation:
- Full sphere potential at center: −2R3GM
- Cavity mass removed: M/27 with its center at OB=2R/3
- Potential due to cavity at center: +18RGM
- Total potential: −2R3GM+18RGM=−9R13GM
