Question
Question: Initially, the switch is in position 1 for a long time and then shifted to position 2 as shown in th...
Initially, the switch is in position 1 for a long time and then shifted to position 2 as shown in the figure. Just after closing the switch, the magnitude of current through the capacitor is:
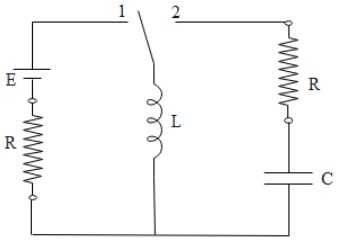
A. zero B. 2RE C. RE D. none of these
Solution
When the switch is kept at position 1 for a long time, it attains a steady state. When the switch is set to position 2, the inductor will not allow the current to change immediately and at first the current in the circuit will remain the same as before.
Complete answer:
We are given a circuit as shown in the given diagram. It is given that the switch is attached to point A for a long time. Due to which the circuit attains a steady state which means that the current in the circuit is at its maximum value and this maximum value of current is simply given by the following expression:
I=RE
Now when the switch is set to position 2, the inductor will not allow the current to change immediately in the circuit and the value of current in the circuit will be the same as the above value in steady state. Since current through all components is the same in a series circuit, the current through the capacitor will also be the same as the steady state current value.
Just after closing the switch, the magnitude of current through the capacitor is:
I=RE
Hence, the correct answer is option C.
Note:
It should be noted that the current will remain steady for only a short duration of time after switching to position 2. It is the property of the inductor to slowly allow the change in the current in the circuit. Eventually, the current will be different in the circuit from the initial steady state value and hence, the current through the capacitor will also change with time and the circuit will again attain a steady state.
