Question

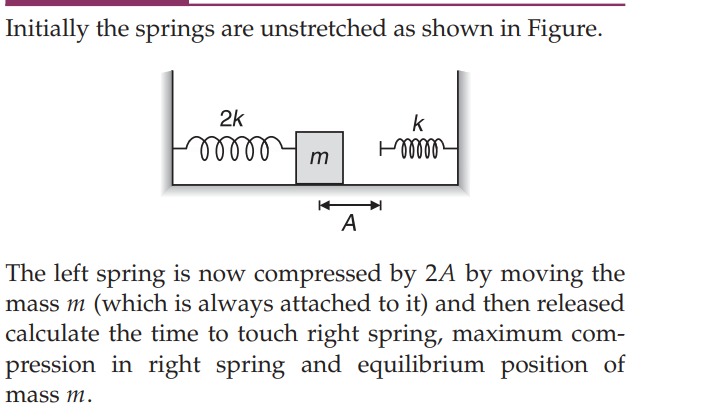
Initially the springs are unstretched as shown in Figure.

The left spring is now compressed by 2A by moving the mass $m$ (which is always attached to it) and then released calculate the time to touch right spring, maximum compression in right spring and equilibrium position of mass $m$.

Answer 1

Time to touch right spring = $\frac{2\pi}{3} \sqrt{\frac{m}{2k}}$, Maximum compression in right spring = $A\left(\frac{\sqrt{22}-2}{3}\right)$, Equilibrium position of mass m = $\frac{A}{3}$

Answer 2

The problem involves two phases of motion for the mass $m$.

1. Phase 1: Motion before touching the right spring

• Initial setup: The mass $m$ is initially at $x=0$, and both springs are unstretched. The right spring is located at $x=A$.

• Compression: The mass is moved to $x=-2A$, compressing the left spring (stiffness $2k$) by $2A$. The right spring is not involved.

• Motion: When released, the mass undergoes Simple Harmonic Motion (SHM) under the influence of the left spring only.

  • The restoring force is $F = -(2k)x$.
  • The angular frequency is $\omega_1 = \sqrt{\frac{2k}{m}}$.
  • The equilibrium position for this phase is $x_{eq1} = 0$.
  • The amplitude of this SHM is $A_1 = 2A$.

• Equation of motion: Since the mass is released from rest at $x=-2A$, the displacement as a function of time is $x(t) = -2A \cos(\omega_1 t)$.

• Time to touch the right spring: The mass touches the right spring when $x(t) = A$.

  • $A = -2A \cos(\omega_1 t)$
  • $\cos(\omega_1 t) = -\frac{1}{2}$
  • The smallest positive value for $\omega_1 t$ is $\frac{2\pi}{3}$.
  • Therefore, the time to touch the right spring is $t = \frac{2\pi}{3\omega_1} = \frac{2\pi}{3\sqrt{2k/m}} = \frac{2\pi}{3} \sqrt{\frac{m}{2k}}$.

• Velocity at the moment of touching:

  • The velocity of the mass is $v(t) = \frac{dx}{dt} = 2A \omega_1 \sin(\omega_1 t)$.
  • At $t = \frac{2\pi}{3\omega_1}$, $\omega_1 t = \frac{2\pi}{3}$.
  • $v_A = 2A \omega_1 \sin\left(\frac{2\pi}{3}\right) = 2A \omega_1 \left(\frac{\sqrt{3}}{2}\right) = A \omega_1 \sqrt{3}$.
  • Substituting $\omega_1$: $v_A = A \sqrt{3} \sqrt{\frac{2k}{m}} = A \sqrt{\frac{6k}{m}}$.

2. Phase 2: Motion after touching the right spring

• Forces: Once the mass touches and compresses the right spring (i.e., for $x > A$), both springs exert forces.
  • Force from the left spring: $F_L = -2kx$.
  • Force from the right spring: $F_R = -k(x-A)$.
  • The net force on the mass is $F_{net} = F_L + F_R = -2kx - k(x-A) = -3kx + kA$.
• New Equilibrium Position: For SHM, the force is of the form $F = -K_{eff}(x - x_{eq})$.
  • Comparing $-3kx + kA$ with $-3k(x - A/3)$, we find:
    • The effective spring constant is $K_{eff} = 3k$.
    • The new equilibrium position is $x_{eq2} = \frac{A}{3}$.
• New Angular Frequency: The angular frequency for this phase is $\omega_2 = \sqrt{\frac{K_{eff}}{m}} = \sqrt{\frac{3k}{m}}$.
• Amplitude of new SHM: The motion starts at $x_i = A$ with velocity $v_i = v_A = A\sqrt{\frac{6k}{m}}$. The amplitude $A_2$ of this new SHM is given by:
  • $A_2 = \sqrt{(x_i - x_{eq2})^2 + \left(\frac{v_i}{\omega_2}\right)^2}$
  • $A_2 = \sqrt{\left(A - \frac{A}{3}\right)^2 + \left(\frac{A\sqrt{6k/m}}{\sqrt{3k/m}}\right)^2}$
  • $A_2 = \sqrt{\left(\frac{2A}{3}\right)^2 + \left(A\sqrt{\frac{6k}{3k}}\right)^2}$
  • $A_2 = \sqrt{\frac{4A^2}{9} + (A\sqrt{2})^2} = \sqrt{\frac{4A^2}{9} + 2A^2} = \sqrt{\frac{4A^2 + 18A^2}{9}} = \sqrt{\frac{22A^2}{9}}$
  • $A_2 = \frac{A\sqrt{22}}{3}$.
• Maximum Compression in right spring: The mass reaches its maximum compression in the right spring when it is at its extreme right position in this new SHM.
  • Maximum position $x_{max} = x_{eq2} + A_2 = \frac{A}{3} + \frac{A\sqrt{22}}{3} = A\left(\frac{1+\sqrt{22}}{3}\right)$.
  • The compression in the right spring is the displacement beyond its natural length ($A$).
  • Compression $= x_{max} - A = A\left(\frac{1+\sqrt{22}}{3}\right) - A = A\left(\frac{1+\sqrt{22}-3}{3}\right) = A\left(\frac{\sqrt{22}-2}{3}\right)$.