Question
Question: Initially spring in its natural length now a block at mass \(0.25\;kg\) is released then find out th...
Initially spring in its natural length now a block at mass 0.25kg is released then find out the maximum force by the system on the floor?
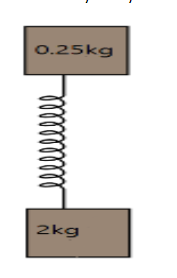
Solution
Here, we need to find the normal force acting on the lower block. Since there is a spring mass system above the lower block we can say that it exerts some force on the lower block. Also the force exerted by the spring mass system is given from Hooke’s law.
Formula: 21kx2=m1gx
Complete answer:
Let us assume that the spring mass system of the given body is isolated. Then we know from Hooke’s law that the magnitude of the force exerted by the spring is directly proportional to the displacement of the spring. It is mathematically expressed as F=−kx, k is the spring constant. The negative sign indicates that the spring is resisting the applied force.
Let us now consider the free body diagram of the lower block of mass m2=2kg, as shown below.
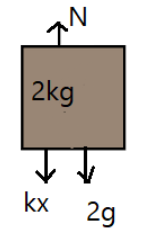
Then we have,
N=kx+m2g
⟹N=kx+2×10
⟹N=kx+20
Also, from work energy theorem, we know that the work done is moving the spring by some x distance due to the force of the spring, results in W=ΔE, where, E is the energy of the system, here we have potential energy. If the spring is in its natural length, then we have, the work done of the upper block of mass m1=0.25kg is given as 21kx2=m1gx
⟹21kx=m1g
kx=2m1g
Substituting, we get, kx=2×0.25×10
⟹kx=5N
Substituting in the normal force, we get
⟹N=5+20=25N
∴N=25N is the required answer.
Note:
The force on the spring is either due to the compression or due to the extension of the spring. We can say that k is a restoring force which tries to restore the spring to its equilibrium position. The spring constant is expressed in terms of N/m .
