Solveeit Logo
Login

Question

Question: Initially car A is \(10.5m\) ahead of car B. Both start moving at time \(t = 0\) in the same directi...

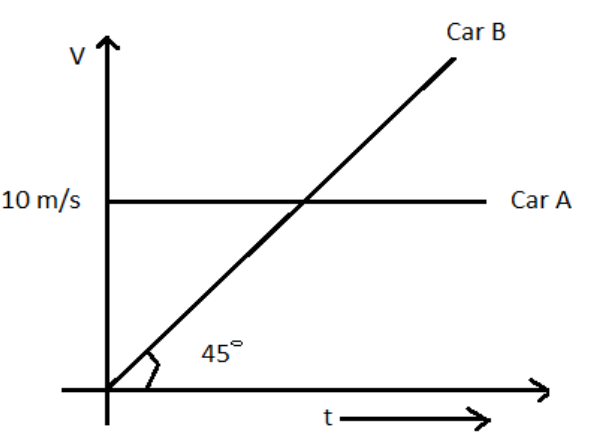
Initially car A is 10.5m10.5m ahead of car B. Both start moving at time t=0t = 0 in the same direction along a straight line. The velocity time graph of two cars shown in figure. The time when the car B will catch the car A, will be:

A. t=21sec⁡t = 21\sec
B. t=25sec⁡t = 2\sqrt 5 \sec
C. 20sec⁡20\sec
D. None of these

Explanation

Solution

We know that equations of motion are equations that are helpful in determination of dynamic variables and behaviour of motion of a system. This problem is solved with the help of equation s=ut+12ats = ut + \dfrac{1}{2}at which gives the distance covered by any object. Here s=s = distance covered, a=a = acceleration, u=u = initial velocity and t=t = time. We can draw graphs of motions with the help of these equations.

Complete answer:
We have studied that the slope of velocity- time graph gives acceleration. We should also take care of the direction of acceleration. Here the given graph is velocity- time graph. Here the given graph is velocity- time graph. Hence the acceleration of Car a and B can be calculated with the help of a given graph. Acceleration of Car A =0m/s2 = 0m/{s^2}and acceleration of Car B =1m/s2 = 1m/{s^2}.Now distance covered by car A and B can be calculated with help of equation s=ut+12ats = ut + \dfrac{1}{2}at. Hence;
If the distance covered by car A and car B are sA{s_A} and sB{s_B} respectively and it is given in the graph that initial velocity is u=10m/su = 10m/s.

sA=ut+12at2 sA=10×t+12×0×t2 sA=10t  {s_A} = ut + \dfrac{1}{2}a{t^2} \\\ {s_A} = 10 \times t + \dfrac{1}{2} \times 0 \times {t^2} \\\ {s_A} = 10t \\\

sB=ut+12at2 sB=0×t+12×1×t2 sB=t22  {s_B} = ut + \dfrac{1}{2}a{t^2} \\\ {s_B} = 0 \times t + \dfrac{1}{2} \times 1 \times {t^2} \\\ {s_B} = \dfrac{{{t^2}}}{2} \\\

It is given in the problem statement that initially car A is 10.5m10.5m ahead of car B so sB−sA=10.5{s_B} - {s_A} = 10.5. Now we will put the value of distances covered by car A and car B in the equation. We will get
t22−10t=10.5\dfrac{{{t^2}}}{2} - 10t = 10.5
t2−20t−21=0{t^2} - 20t - 21 = 0
t=21sec⁡,−1sec⁡t = 21\sec , - 1\sec
As we know that time cannot be negative, so t = 21. The time when car B will catch car A is t=21sec⁡t = 21\sec .

So, the correct answer is “Option A”.

Note:
We have solved this question with the help of the equation of motion. Some important points were given in the problem statement which help in finding the time when the car B will catch the car A. We know that acceleration is a vector quantity so we should always be aware of the direction of the acceleration.