Question

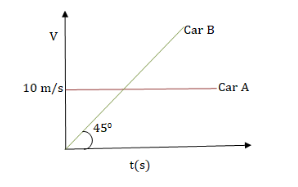
Initially, car A is $10.5\,{\text{m}}$ ahead of car B. Both start moving at time $t = 0$ in the same direction along a straight line. The velocity-time graph of two cars is shown in the figure. The time when the car B will catch the car A, will be

A. $21\,{\text{s}}$
B. $22\,{\text{s}}$
C. $21\sqrt 2 \,{\text{s}}$
D. $12\,{\text{s}}$

Answer 1

Observe carefully the given conditions, and then make a neat diagram representing the given problem. Using the given graph, find the velocity of car A. Find the distance car B and car A would travel to get to the point where they would meet. Use these values to calculate the required time.

Complete step by step answer:
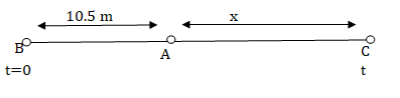
Given, car A is ahead of car B by $10.5\,{\text{m}}$.
Both the cars start from $t = 0$ that is, initial velocities of car A and car B is zero.
${u_A} = {u_B} = 0$
Let C be the point where the both cars meet or where car B catches car A at time $t$ and let $x$ be the distance between the point when the both cars meet and the starting point of car A. Let us draw a diagram for the given situation.

From the graph of velocity vs time in the question, we observe that car A is moving with constant velocity, ${v_A} = 10\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$
We have the formula for distance as, ${\text{distance}} = {\text{speed}} \times {\text{time}}$
So, $x$ can be written as,
$x = {v_A}t$
Putting the value of ${v_A}$, we get
$x = 10t$ (i)

Velocity of car B is changing with time and acceleration of car B will be the slope of velocity vs time graph, which is given here as,
$a = \dfrac{{dv}}{{dt}} = \tan {45^ \circ } = 1$
Now, we find the time at which car B will reach point C.
Distance between car B and point C is $s = 10.5 + x$
Using equation of motion, we have
$s = {u_B}t + \dfrac{1}{2}a{t^2}$
Putting the values of $s$, $a$ and ${u_B}$, we get
$10.5 + x = \dfrac{1}{2}(1){t^2}$

\Rightarrow {t^2} - 2x - 21 = 0 $$ Putting the value of $$x$$ from equation (i), we get $${t^2} - 20t - 21 = 0 \\\ \Rightarrow {t^2} - 21t + t - 21 = 0 \\\ \Rightarrow t(t - 21) + (t - 21) = 0 \\\ \Rightarrow t = 21, - 1 $$ The value of time cannot be negative so, $$t = 21\,{\text{s}}$$. Therefore, the time at which car B reaches car A is $$21\,{\text{s}}$$ **Hence, the correct answer is option A.** **Note:** For such problems, always draw a diagram using the given assumptions or conditions, as this would make it easy for you to visualize the problem. For questions involving distance, velocity, acceleration or time always remember the equations of motions. Applying the given conditions and using equations of motion, you can calculate the value of the required quantity.