Question

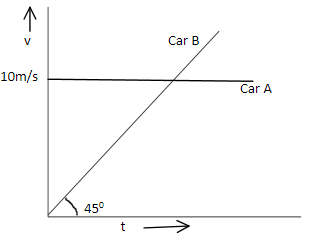
Initially car A is $10.5$ m ahead of car B. Both start moving at time $t = 0$ in the same direction along a straight line. The velocity time graph of two cars is shown in figure. The time when the car B catches the car A will be:

(A) $t = 21$
(B) $t = \dfrac{2}{5}$
(C) $t = 20$
(D) None of the above.

Answer 1

Hint : Here, study the given diagram. Use the kinematic equations to find out distance of car B, also use $a=tan45^0$ as this is the way to find acceleration. If needed use basic formulas of velocity, distance and time.

Complete Step By Step Answer:
velocity of car A, ${v_A} = 10.5m{s^{ - 1}}$
Let us now find out the distance travelled by Car A in $t$ sec, ${s_A}$ be the distance travelled by car A.
Therefore, ${s_A} = 10t$
Distance travelled by Car B, distance be ${s_B}$
${s_B} = \dfrac{1}{2}{t^2}$ (Using formula of kinematic equation, $s = ut + \dfrac{1}{2}a{t^2}$ and $a = \tan {45^0}$ )
Now, as per the given condition that the Car A is $10.5$ m ahead of Car B, we have
${s_A} + 10.5 = \dfrac{1}{2}{t^2}$
$\Rightarrow 10.5 + 10t = \dfrac{1}{2}{t^2}$
$\Rightarrow {t^2} - 20t - 21 = 0$
$\Rightarrow t = \dfrac{{20 \pm \sqrt {{{(20)}^2} - 4( - 21)} }}{2}$ (using, $\dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$ )
$\Rightarrow t = 21$ sec
Thus the time taken by car B to catch car A is $21$ seconds.
Option A is the correct answer.

Note :
As we know that velocity of any body is the result of distance travelled by the boy with respect to time. Here, car A is running forward of car B to catch car A, it has to cover the difference between them in seconds. Finding out distance travelled by car B is not necessary as we have to use a kinematical equation to find time taken.