Question

Initially 100 µF is charged by 200 V then switch S₁ is closed for some time & then opened & then S₂ is closed for some time & it is opened then 400 µF is found to charge by 100 V. Then find minimum time (in sec) for which S₂ is closed for this process to happen. If answer in ($\frac{\pi}{n}$), fill n.

Answer 1

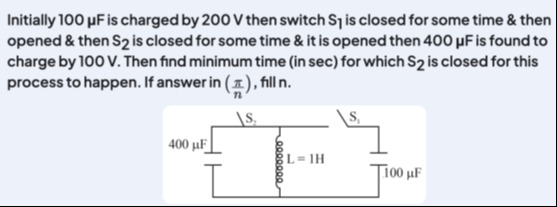
100

Answer 2

Solution:

1. Stage‐1 (S₁ closed): – We use the LC circuit of the 100 µF capacitor (initially charged to 200 V) and the 1 H inductor. – For an LC circuit the maximum inductor current is reached at a quarter‐cycle. – The angular frequency is

   $$\omega_1=\frac{1}{\sqrt{L\,C_1}}=\frac{1}{\sqrt{1\times 100\times10^{-6}}}=\frac{1}{0.01}=100\;{\rm rad/s}.$$

   – Thus the required time to reach maximum current is

   $$t_1=\frac{\pi}{2\omega_1}=\frac{\pi}{2\times100}=\frac{\pi}{200}\;{\rm s}.$$

   At that moment the inductor current becomes

   $$i_0=200\,\sqrt{C_1/L}=200\times\sqrt{100\times10^{-6}}=200\times0.01=2\;{\rm A}.$$

   We then open S₁ so that nearly the full energy (energy of 2 A inductor current) is isolated.

2. Stage‐2 (S₂ closed): – Now S₂ is closed to connect the inductor (with initial current 2 A) to the 400 µF capacitor (which is initially uncharged). – For the LC circuit of $C_2=400\times10^{-6}\,{\rm F}$ and $L=1\,{\rm H}$ the angular frequency is

   $$\omega_2=\frac{1}{\sqrt{L\,C_2}}=\frac{1}{\sqrt{1\times400\times10^{-6}}}=\frac{1}{0.02}=50\;{\rm rad/s}.$$

   – With initial conditions $V(0)=0$ and $i(0)=2$ A the capacitor voltage will build up as

   $$V_{C_2}(t)=\left(i_0\sqrt{\frac{L}{C_2}}\right)\sin(\omega_2t)=\left(2\times\frac{1}{0.02}\right)\sin(50t)=100\,\sin(50t).$$

   The maximum voltage (i.e. 100 V) is reached when $\sin(50t)=1$, i.e. at

   $$50t=\frac{\pi}{2}\quad\Longrightarrow\quad t=\frac{\pi}{100}\;{\rm s}.$$

Thus the minimum time for which S₂ must remain closed is $\pi/100$ sec. In the answer format $\pi/n$, we have $n=100$.