Question
Question: Initial and final pressures and volumes of a gas in a thermodynamic process are \({P_i}\), \({V_i}\)...
Initial and final pressures and volumes of a gas in a thermodynamic process are Pi, Vi and Pf, Vf, respectively. If PVn=constant, then the amount of work done is:
(A) minimum for n=γ
(B) minimum for n=1
(C) minimum for n=0
(D) minimum for n=γ1
Solution
Here the initial and final pressure and volume are given. Using the equation of the gas, plot the graph of pressure versus volume for different values of n . The area under the graph pressure versus volume gives the work done by the gas. Then using the graph determine the minimum work done by the gas. Here the given thermodynamic process is an adiabatic process.
Complete step by step answer:
A system undergoing physical changes in such a way that neither the heat is allowed to enter the system from the surrounding nor allowed to leave the system to the surrounding is called the adiabatic process. In adiabatic compression, the temperature increases as work is done on the gas. In adiabatic expansion, the temperature decreases as the work is done by the gas.
We know that
PVn= constant
P=VnC
Where C is a constant,P is the pressure,V is the volume.
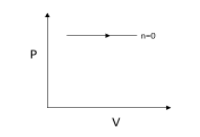
Now for n=0, we get
P=V0C=C
The pressure is constant since P=C.
Now let us substitute n=1, we get P=VC
Here we obtain a rectangular hyperbola since the pressure is inversely proportional to volume.
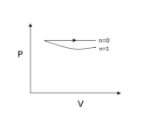
Now n=γ, we get
P=VγC
We know that the adiabatic constant γ is greater than one, we can write
Vγ>V
And we can also write
VγC<VC−−−−−(1)
From the above equation, I can also write
Vγ1C>VC−−−−−(2)
From comparing the two-equation we can write
VγC<Vγ1C
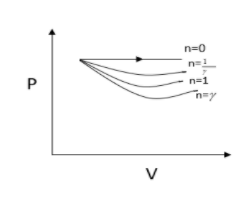
Here work done is given by the area under the curve. It is clear that work is done is minimum for n=γ
Hence option(A)is the correct option.
Note: Pressure, Volume, Temperature changes suddenly from P1 , V1,T1 to P2,V2 T2 if a gas is compressed suddenly in the thermally insulated flask. This is an adiabatic process. In adiabatic compression, the temperature increases as work is done on the gas. In adiabatic expansion, the temperature decreases as the work is done by the gas. A system undergoing physical changes in such a way that neither the heat is allowed to enter the system from the surrounding nor allowed to leave the system to the surrounding is called the adiabatic process.
