Question

If $\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix} A \begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$, then the value of matrix $A =$

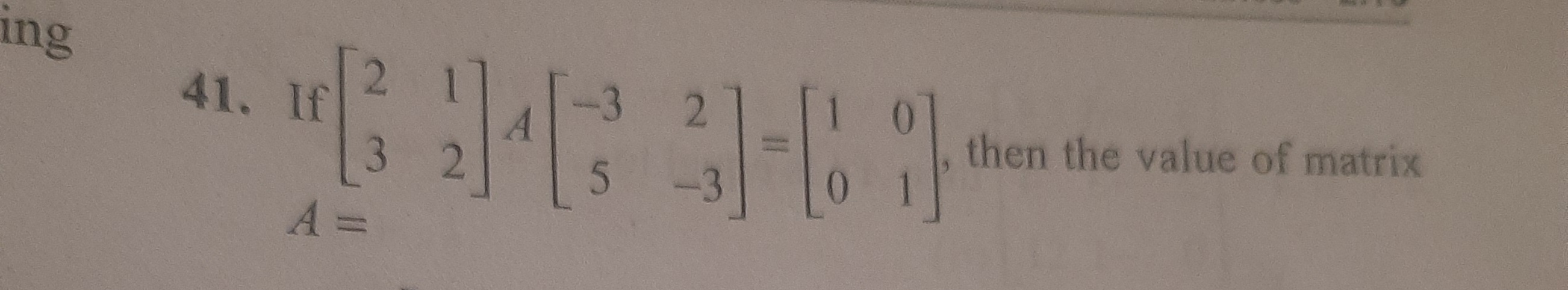
Answer 1

$\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}$

Answer 2

Given $M A N = I$, we have $A = M^{-1} N^{-1}$. Compute inverses:

$$M^{-1} = \begin{bmatrix} 2 & -1 \\ -3 & 2 \end{bmatrix}, \quad N^{-1} = \begin{bmatrix} 3 & 2 \\ 5 & 3 \end{bmatrix}.$$

Multiply to get:

$$A = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}.$$