Solveeit Logo
Login

Question

Question: If $\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix} A \begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix} = ...

If [2132]A[−325−3]=[1001]\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix} A \begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, then the value of matrix A=A =

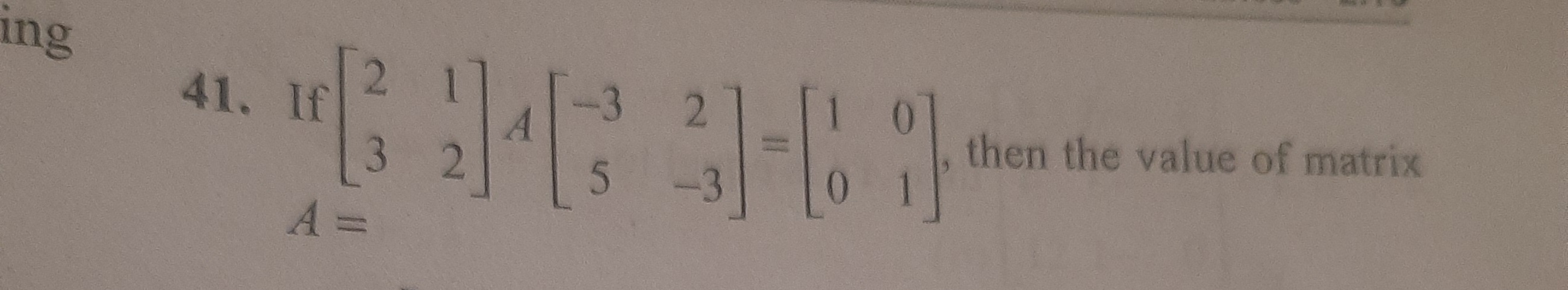
Answer

[1110]\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}

Explanation

Solution

Given

[2132]A[−325−3]=I.\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix} A \begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix} = I.

Let B=[2132]B = \begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix} and C=[−325−3]C = \begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix}. Then

BAC=I  ⟹  A=B−1C−1.B A C = I \implies A = B^{-1} C^{-1}.
  1. Find B−1B^{-1}:

The determinant of BB is:

det⁡(B)=(2)(2)−(3)(1)=4−3=1.\det(B) = (2)(2) - (3)(1) = 4-3=1.

Hence,

B−1=[2−1−32].B^{-1} = \begin{bmatrix} 2 & -1 \\ -3 & 2 \end{bmatrix}.
  1. Find C−1C^{-1}:

For C=[−325−3]C=\begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix},

det⁡(C)=(−3)(−3)−(5)(2)=9−10=−1.\det(C) = (-3)(-3) - (5)(2) = 9-10=-1.

Using the formula for the inverse,

C−1=1det⁡(C)[−3−2−5−3]=−[−3−2−5−3]=[3253].C^{-1} = \frac{1}{\det(C)} \begin{bmatrix} -3 & -2 \\ -5 & -3 \end{bmatrix} = -\begin{bmatrix} -3 & -2 \\ -5 & -3 \end{bmatrix} = \begin{bmatrix} 3 & 2 \\ 5 & 3 \end{bmatrix}.
  1. Calculate A=B−1C−1A = B^{-1} C^{-1}:
A=[2−1−32][3253].A = \begin{bmatrix} 2 & -1 \\ -3 & 2 \end{bmatrix} \begin{bmatrix} 3 & 2 \\ 5 & 3 \end{bmatrix}.

Multiply the matrices:

A11=2⋅3+(−1)⋅5=6−5=1,A12=2⋅2+(−1)⋅3=4−3=1,A21=(−3)⋅3+2⋅5=−9+10=1,A22=(−3)⋅2+2⋅3=−6+6=0.\begin{aligned} A_{11} &= 2\cdot 3 + (-1)\cdot 5 = 6-5 = 1,\\[1mm] A_{12} &= 2\cdot 2 + (-1)\cdot 3 = 4-3 = 1,\\[1mm] A_{21} &= (-3)\cdot 3 + 2\cdot 5 = -9+10 = 1,\\[1mm] A_{22} &= (-3)\cdot 2 + 2\cdot 3 = -6+6 = 0. \end{aligned}

Thus,

A=[1110].A = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}.