Question
Question: If $\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix} A \begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix} = ...
If [2312]A[−352−3]=[1001], then the value of matrix A=
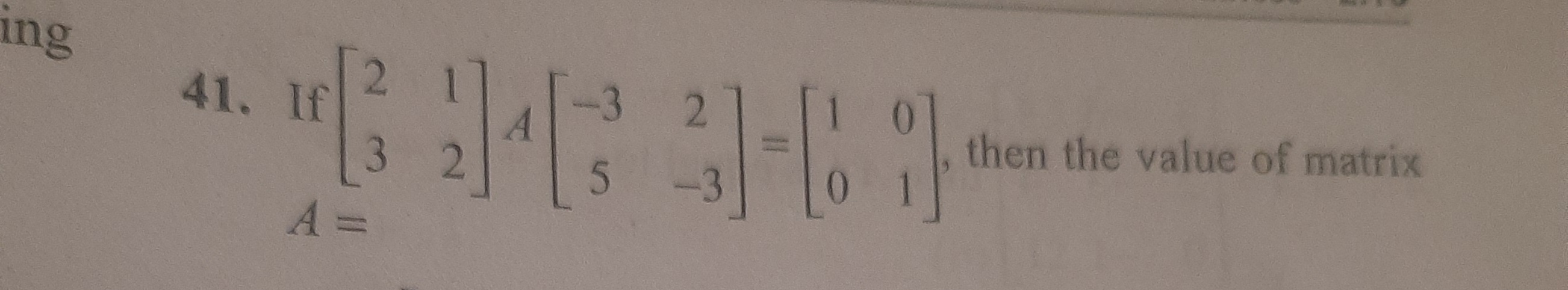
[1110]
Solution
To find the matrix A, we need to isolate it from the given equation:
[2312]A[−352−3]=[1001]
Let P=[2312] and Q=[−352−3]. Then the equation can be written as PAQ=I, where I is the identity matrix. To solve for A, we need to find the inverses of P and Q and multiply them appropriately:
A=P−1Q−1
Step 1: Find P−1
The determinant of P is: det(P)=(2)(2)−(1)(3)=4−3=1
Thus, the inverse of P is: P−1=[2−3−12]
Step 2: Find Q−1
The determinant of Q is: det(Q)=(−3)(−3)−(2)(5)=9−10=−1
Thus, the inverse of Q is: Q−1=−11[−3−5−2−3]=[3523]
Step 3: Compute A=P−1Q−1
Now, multiply P−1 and Q−1: A=[2−3−12][3523]
Calculating the product: A=[(2∗3+(−1)∗5)(−3∗3+2∗5)(2∗2+(−1)∗3)(−3∗2+2∗3)]=[6−5−9+104−3−6+6]=[1110]
Therefore, A=[1110].
