Question

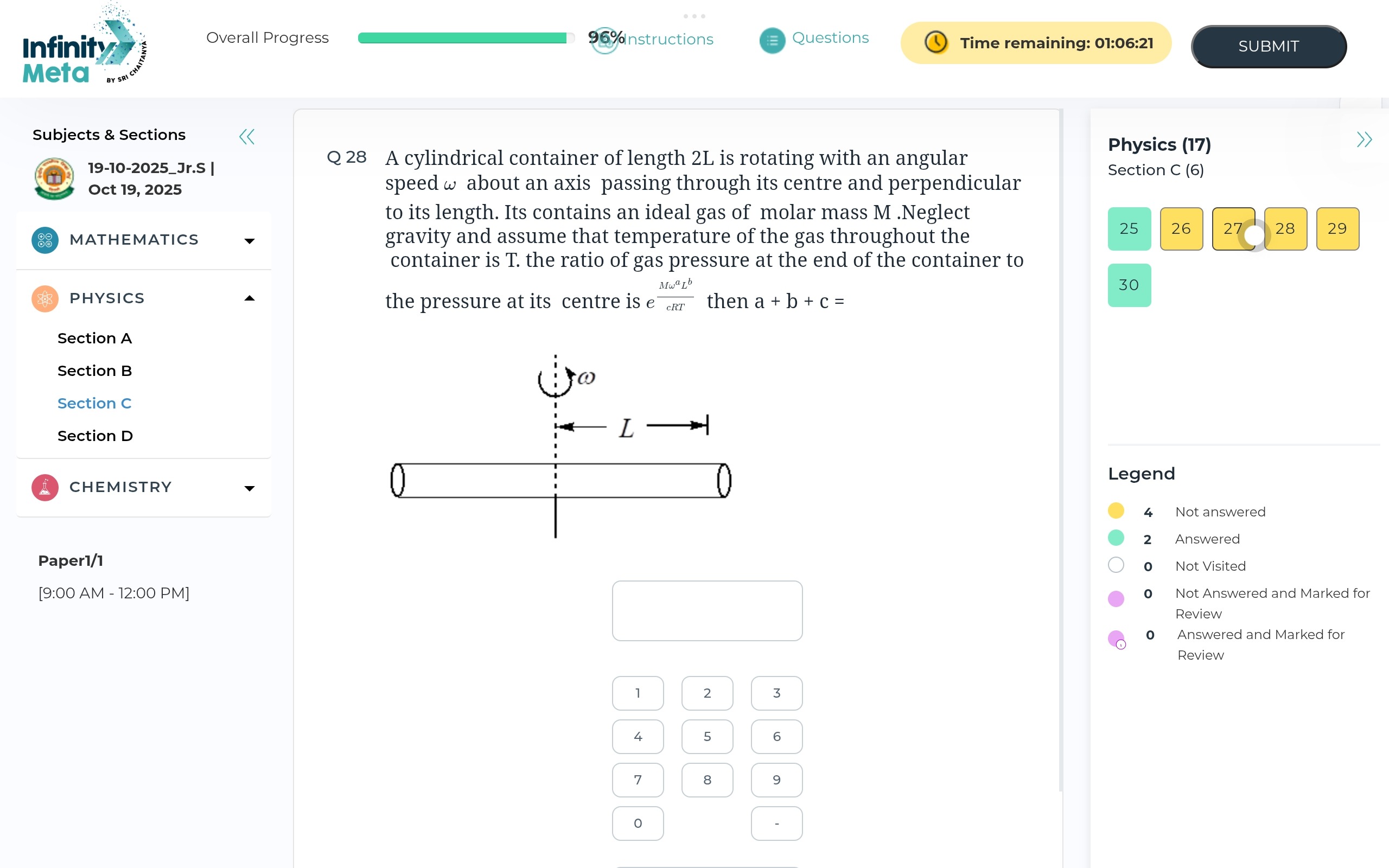
A cylindrical container of length 2L is rotating with an angular speed $\omega$ about an axis passing through its centre and perpendicular to its length. It contains an ideal gas of molar mass M. Neglect gravity and assume that temperature of the gas throughout the container is T. the ratio of gas pressure at the end of the container to the pressure at its centre is $e^{\frac{M\omega^a L^b}{cRT}}$ then a + b + c =

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5
• F. 6

Answer 1

Answer: (F)

6

Answer 2

The centrifugal force on a gas element is $dF_c = dm \cdot \omega^2 r$. For a gas element of mass $dm$ at distance $r$, the pressure difference is $dP \cdot A = dF_c$. Using the ideal gas law $\rho = MP/RT$, we get $dP/P = (M\omega^2/RT) r dr$. Integrating from the center ($r=0$) to the end ($r=L$), we get $\ln(P_{end}/P_{center}) = M\omega^2 L^2 / (2RT)$. Comparing this with the given expression $e^{\frac{M\omega^a L^b}{cRT}}$, we find $a=2$, $b=2$, and $c=2$. Thus, $a+b+c = 2+2+2 = 6$.