Question

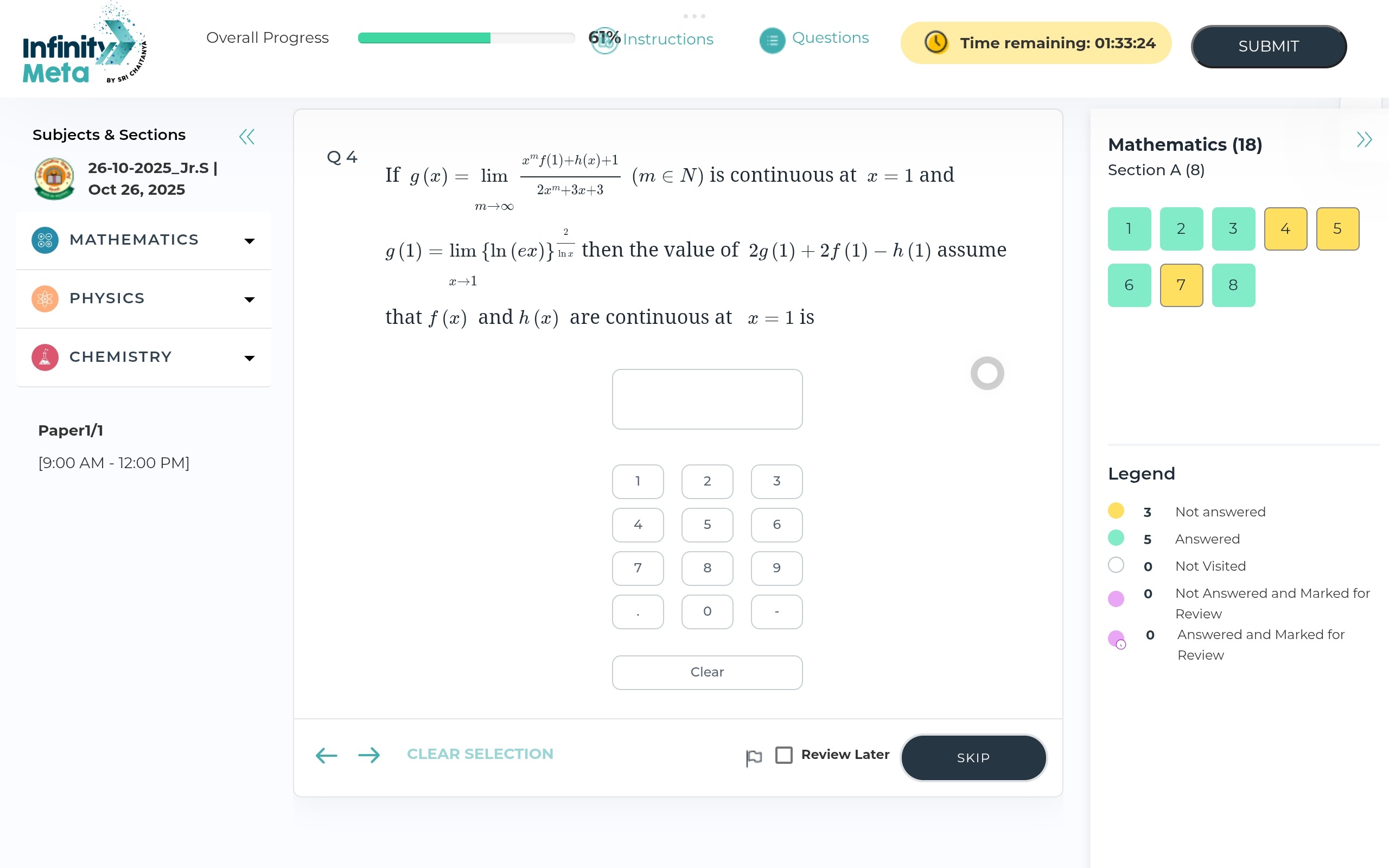
If $g(x) = \lim_{m\to\infty} \frac{x^m f(1)+h(x)+1}{2x^m+3x+3} (m \in N)$ is continuous at x = 1 and $g(1) = \lim_{x\to 1} \{\ln (ex)\}^{\frac{2}{\ln x}}$ then the value of $2g(1) + 2f(1) - h(1)$ assume that $f(x)$ and $h(x)$ are continuous at $x = 1$

Answer 1

1

Answer 2

For $x > 1$, $g(x) = \frac{f(1)}{2}$. Thus, $\lim_{x\to 1^+} g(x) = \frac{f(1)}{2}$. For $0 \le x < 1$, $g(x) = \frac{h(x)+1}{3x+3}$. Since $h(x)$ is continuous at $x=1$, $\lim_{x\to 1^-} g(x) = \frac{h(1)+1}{3(1)+3} = \frac{h(1)+1}{6}$. Since $g(x)$ is continuous at $x=1$, $\frac{f(1)}{2} = \frac{h(1)+1}{6} = g(1)$. This gives $f(1) = 2g(1)$ and $h(1) = 6g(1) - 1$.

To find $g(1)$, let $y = \{\ln (ex)\}^{\frac{2}{\ln x}}$. $\ln y = \frac{2}{\ln x} \ln(\ln(ex))$. Using L'Hopital's Rule: $\lim_{x\to 1} \ln y = \lim_{x\to 1} \frac{2 \cdot \frac{1}{\ln(ex)} \cdot \frac{1}{x}}{\frac{1}{x}} = \lim_{x\to 1} \frac{2}{\ln(ex)} = \frac{2}{\ln(e)} = 2$. So, $g(1) = e^2$.

The expression to evaluate is $2g(1) + 2f(1) - h(1)$. Substituting the relations: $2g(1) + 2(2g(1)) - (6g(1) - 1) = 2g(1) + 4g(1) - 6g(1) + 1 = 1$.