Question
Question: Infinite rods of uniform mass density and length \[{\text{L, }}\dfrac{{\text{L}}}{2},{\text{ }}\dfra...
Infinite rods of uniform mass density and length L, 2L, 4L......are placed one upon another up to infinite as shown in the figure. Find the x-coordinate of the center of mass.
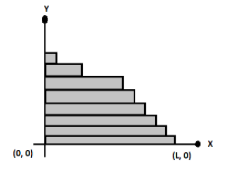
A. 0
B. 3L
C. 2L
D. 32L
Solution
The point at which the whole mass of the system is concentrated is defined as the center of mass of a particle. If we have the data of the masses and the coordinates of the particles of an n-particle system.
Formulas used:
The coordinates of the center of mass of this system can be expressed as:
-XCOM=∑mii=1∑nmixi
-YCOM=∑mii=1∑nmiyi
Complete step by step answer:
x coordinate of Centre of mass is given by
XCOM=∑mii=1∑nmixi
The numerator is
i=1∑nmixi=m2L+2m(4L)+......
The denominator is,
∑mi=m+2m+4m+......
So, XCOM=∑mii=1∑nmixi=m+2m+4m+......m2L+2m(4L)+......
XCOM=m(1+21+41+......)mL(21+81+321+....)
XCOM=(1−21)1L1−4121
XCOM=2L(64)=3L
Hence, B option is correct
Additional information:
A large number of problems involving extended bodies or real bodies of finite size can be solved by taking them as Rigid Bodies. We define a rigid body as a body having a definite and unchanging shape.
Rigid body: It is a rigid assembly of particles with a fixed inter-particle distance.
Centre of mass for some bodies:
-A plane lamina - Point of intersection of diagonals
-Triangular plane lamina - Point of intersection of medians
-Rectangular or cubical block - Points of intersection of diagonals
-Hollow cylinder - Middle point of the axis of a cylinder
Note:
-The center of mass and center of gravity both are different.
-Centre of a mass of a body in which the total mass of the body is concentrated at one point.
-Where the center of gravity is the point at which the resultant of all gravitational forces on all the particles of the body acts.
-But for many objects, these two points are exactly in the same place when the gravitational field is uniform across the object.
