Question

Infinite number of flasks is connected to one another as shown above. The volume and pressure in each flask vary as shown. The stopcocks are initially closed. Then common pressure, when all the stopcocks are opened is (Assume constant temperature)

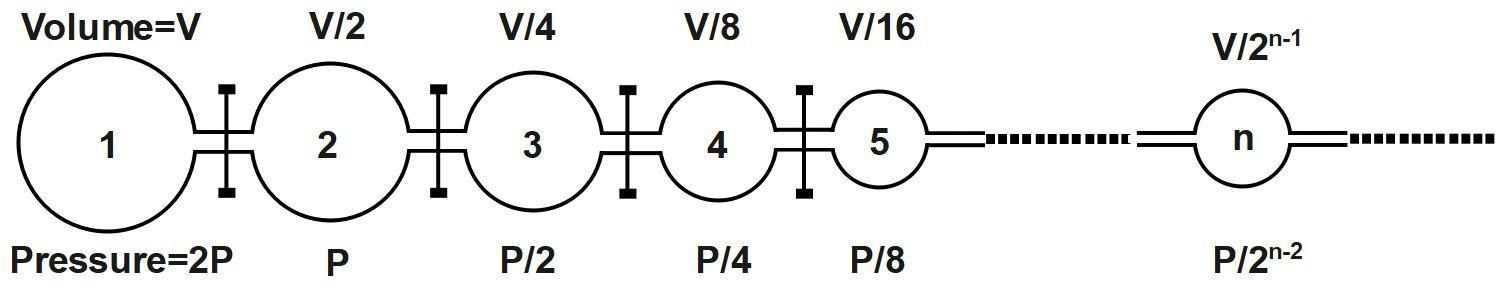
(A) $P$
(B) $\dfrac{P}{2}$
(C) $\dfrac{P}{4}$
(D) $\dfrac{4}{3}P$

Answer 1

We know that the state function is the property of a system which does not depend on the path followed by the system and depends only on the initial and final state of the system. These particles only interact with one another through elastic collisions. It is easy to define ideal gas, but the ideal gas meaning extends beyond that.

Complete answer:
This concept of the ideal gas formula is important as it obeys all ideal gas law equations, provides a simple equation of state, and is also amenable to analysis by employing statistical mechanisms. A thermodynamic system can be described by a number of thermodynamic parameters such as pressure, volume, temperature, internal energy, enthalpy etc.
These can be divided into state functions and path functions. A state function is a property of a system whose value depends upon the initial and final states of the system. It is also known as point function. These types of functions describe an equilibrium state of a function and do not depend on how the system arrived in that state. For example, Internal energy is considered as a state function and is independent of the path followed to change the state of the system. It is the total energy of a system. This is made up of a number of components such as translational kinetic energy of molecules, bond energy, electronic energy, intermolecular interaction energy of the constituent’s particles of the system etc. Internal energy is a function of pressure, volume, temperature etc. These all variables are state functions.
Here, we have ${{n}_{T}}={{n}_{1}}+{{n}_{2}}+{{n}_{3}}+.....$ similarly $\dfrac{{{P}_{T}}{{V}_{T}}}{RT}=\dfrac{{{P}_{1}}{{V}_{1}}}{RT}+\dfrac{{{P}_{2}}{{V}_{2}}}{RT}+......=\sum{{{P}_{1}}{{V}_{1}}}$
$\therefore {{P}_{T}}{{V}_{T}}=\sum{{{P}_{1}}{{V}_{1}}}$
On further solving we get;
$\therefore {{P}_{T}}{{V}_{T}}=2PV+\dfrac{PV}{2}+\left( \dfrac{P}{2}\times \dfrac{P}{4} \right)+\left( \dfrac{P}{4}\times \dfrac{P}{8} \right)+.......=2PV\left[ 1+\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{1}{46}+....... \right]$
Thus, we get; ${{P}_{T}}{{V}_{T}}=2PV\times \dfrac{1}{1-\dfrac{1}{4}}=2PV\times \dfrac{4}{3}$
$\Rightarrow {{P}_{T}}{{V}_{T}}=2PV\times \dfrac{4}{3}$
As we know that $VT={{V}_{1}}+{{V}_{2}}+{{V}_{3}}+.....=V+\dfrac{V}{2}+\dfrac{V}{4}+\dfrac{V}{8}+.......$
Thus, we get; ${{V}_{T}}=V\left[ 1+\dfrac{1}{2}+...... \right]=V\dfrac{1}{1-\dfrac{1}{2}}=2V$
$\Rightarrow {{V}_{T}}=2V$
Therefore on substitution we get the value of ${{P}_{T}}$ here;
${{P}_{T}}2V=2PV\times \dfrac{4}{3}\Rightarrow {{P}_{T}}=P\times \dfrac{4}{3}$
$\therefore {{P}_{T}}=\dfrac{4}{3}P$
Therefore, the correct answer is option D.

Note:
Remember that the state function includes mass, volume, pressure, temperature, density, entropy etc. There are some variables that depend upon the amount of matter present. These are known as Extensive properties. Examples include mass, volume etc.