Question
Question: Infinite current-carrying conductor \[PQ\] . \(AB\) and \(CD\) are smooth conducting rods on which a...
Infinite current-carrying conductor PQ . AB and CD are smooth conducting rods on which a conductor EF moves with constant velocity V as shown in the figure. The force needed to maintain a constant speed EF is
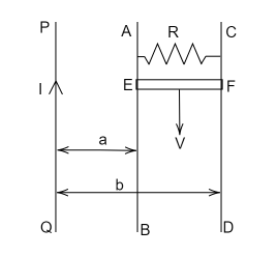
Solution
Find the magnetic field due to the current-carrying wire. Use this magnetic field equation to find the induced emf between EF . Using Ohm’s law, find the current in the loop and hence find the force required to maintain the constant speed.
Complete Step by step solution:
The equation for the magnetic field around the current-carrying wire at a distance r is given by
⇒ B=2πrμoI
Emf induced by the current-carrying rod PQ on the rod EF is given by
⇒ emf=a∫bBVdr
Substituting the already written equation for the magnetic field into the above equation, we get
⇒ emf=a∫b2πrμoIVdr
After integration and substituting the lower and upper limit into the integrated term, we get
⇒ emf=2πμoIVln(ab)
By Ohm's law,
I=RV
Therefore, using OHM’s law, we get the current due to induced emf as
i=Remf
By substituting the derived equation for emf in the above equation for current, we get
⇒ i=2πRμoIVln(ab)
Now, the force on the induced current-carrying rod due to the magnetic field produced due to the current flowing through the rod PQ is given by
⇒ F=a∫bBidr
By substituting the equations for the magnetic field and the induced current, we get
F=a∫b2πrμoI2πRμoIVln(ab)dr
Integrating the above equation and substituting the upper and lower limits to the integrated equation gives us
⇒ F=RV(2πμoIln(ab))2
This is the force required to move the rod EF at a constant velocity V .
Note:
Force on a current-carrying conductor is given by
F=BILsinθ
Here, θ is the angle subtended between the conductor and the direction of the magnetic field. In the given question, the angle between the conductor and the magnetic field is found to be 90∘ . So, sinθ becomes 1 and that is the reason we don’t see the sine term in the equation.
