Question

Inductors in series ?

Answer 1

As we know that current in series combination stays the same, but the voltage across each inductor can be different. The sum of the potential difference (voltage) is equal to the total voltage.

Complete step by step answer:
Inductor: It is an electrical device which is used in electrical circuits for its property of inductance (it is a property by virtue of which a circuit opposes the change in the value of a time varying current flowing through it. It causes opposition only to varying current and does not cause any opposition to steady current.)

Inductance is of two types:
Self-inductance: An electric current flowing around a circuit produces a magnetic field and hence magnetic flux to the current is known as self-inductance, mathematically represented as: $L=\dfrac{\varphi }{i}$.

Mutual inductance: It is defined as the emf induced in one coil opposes the change of current and voltage in the other coil. Which means that two coils are magnetically linked together due to change in magnetic flux. The current present in the inductor stays the same but voltage may vary across each inductor, and the sum of potential difference (voltage) is equal to total voltage.Inductors in series,
${{L}_{eq}}={{L}_{1}}+{{L}_{2}}+{{L}_{3}}+{{L}_{4}}+.......$

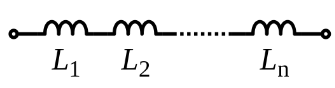
Proof: Applying KVL in the above diagram:
${{V}_{T}}={{V}_{1}}+{{V}_{2}}+{{V}_{3}}+{{V}_{4}}+....eq(i) \\\ V=L\dfrac{dI}{dt}.......eq(ii)$
Putting value of eq(ii) in eq(i), we get:
${{L}_{T}}\dfrac{dI}{dt}={{L}_{1}}\dfrac{dI}{dt}+{{L}_{2}}\dfrac{dI}{dt}+{{L}_{3}}\dfrac{dI}{dt}+{{L}_{4}}\dfrac{dI}{dt}.........$eq(iii)
Dividing the eq(iii) by $\dfrac{dI}{dt}$ we get,
$\therefore {{L}_{eq}}={{L}_{1}}+{{L}_{2}}+{{L}_{3}}+{{L}_{4}}+.......$

Note: To find the total inductance in a circuit (inductors present in series combination) you have to simply add all the inductors and for parallel combination you have to first reciprocal the inductors and then add it simply($\dfrac{1}{{{L}_{eq}}}=\dfrac{1}{{{L}_{e1}}}+\dfrac{1}{{{L}_{e2}}}+\dfrac{1}{{{L}_{3}}}+\dfrac{1}{{{L}_{4}}}+\dfrac{1}{{{L}_{5}}}....$).