Question

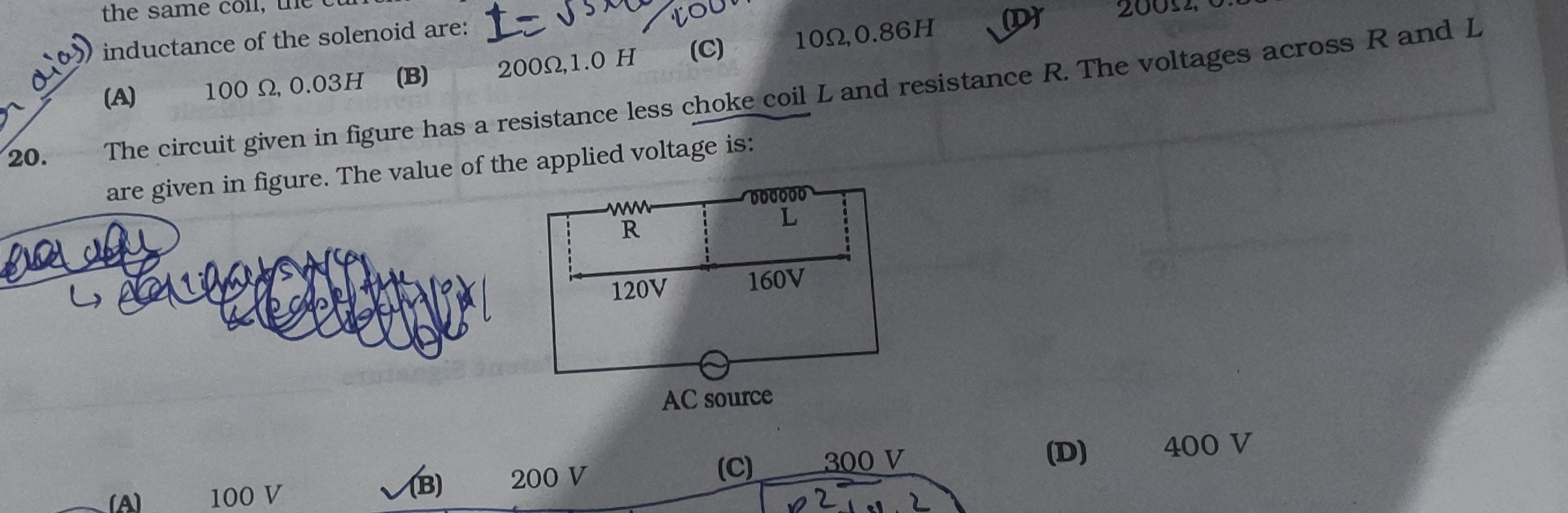
The circuit given in figure has a resistance less choke coil L and resistance R. The voltages across R and L are given in figure. The value of the applied voltage is:

• A. 100 V
• B. 200 V
• C. 300 V
• D. 400 V

Answer 1

Answer: (B)

200 V

Answer 2

The circuit described is a series R-L AC circuit. In a series AC circuit, the current through all components is the same. However, the voltages across the resistor (R) and the inductor (L) are out of phase with each other.

1. Voltage across the resistor ($V_R$): This voltage is in phase with the current flowing through the circuit.
2. Voltage across the inductor ($V_L$): This voltage leads the current by 90 degrees.

Since $V_R$ and $V_L$ are 90 degrees out of phase, the total applied voltage ($V_{applied}$) is the phasor sum of $V_R$ and $V_L$. This can be calculated using the Pythagorean theorem, similar to finding the hypotenuse of a right-angled triangle where $V_R$ and $V_L$ are the perpendicular sides.

The formula for the applied voltage in a series R-L circuit is: $V_{applied} = \sqrt{V_R^2 + V_L^2}$

Given values from the figure: Voltage across resistance, $V_R = 120 \, V$ Voltage across inductance, $V_L = 160 \, V$

Substitute these values into the formula: $V_{applied} = \sqrt{(120 \, V)^2 + (160 \, V)^2}$ $V_{applied} = \sqrt{14400 \, V^2 + 25600 \, V^2}$ $V_{applied} = \sqrt{40000 \, V^2}$ $V_{applied} = 200 \, V$

Thus, the value of the applied voltage is 200 V.