Question

Indicate how many stereoisomers are possible for square planar $[Pt{(N{H_3})_2}\,Br\,Cl]$ ?

Answer 1

Whenever you are trying to count the number of stereoisomers then keep in mind that there must be a difference in positions of ligands when we look at it in three dimensions. Stereoisomers are structures having the same formula but there is a different arrangement of atoms in space, if so they are called to be stereoisomers.

Complete step-by-step answer: We get an idea about the definition of stereoisomers, whenever there is difference in three dimensional arrangement of atoms they possess different stereos in space. There are two possibilities of stereoisomers one is geometrical isomers having cis and trans form, other one is optical isomers which should not have any symmetries. In square planar complexes as all are in planes so they don’t possess any optical isomers.
For the example given above of platinum salt, it is given that this compound is having square planar geometry hence we know that all the ligands should be in one plane that’s why it is called planar and are arranged like four corner of a square at right angle. These two requirements are satisfied when platinum is in center and all other ligands are by side of it making an angle of ${90^ \circ }$ with each other.
Let’s start arranging them like the above conditions- Case $1$ is when both ammonia are cis to each other.


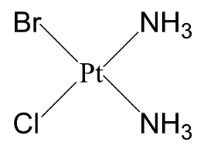
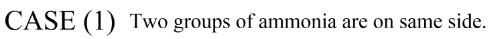
In this structure of case $2$ there is one geometrical isomer is possible and another structure is when both ammonia molecules are in Trans position.


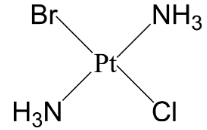
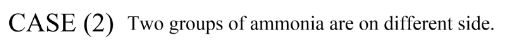
So counting both we have two stereoisomers for the complex of platinum $[Pt{(N{H_3})_2}\,Br\,Cl]$ .

Note: Many students do the same mistake when they count the optical isomer taking case of cis one as optically active but it is not active. Also if it is not giving any planar type of complex, then you have to count the optical isomers when two same ligands are not present at ${180^ \circ }$ , the structure in which ligands are present at ${180^ \circ }$ they have plane of symmetry in them and hence are optically inactive.