Question

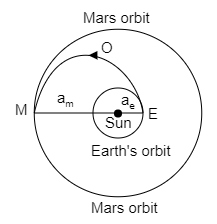
India’s Mangalyaan was sent to the mars by launching it into a transfer orbit EOM around the sun. It leaves the earth at E and meets mars at M. If the semi major axis of Earth’s orbit is ${a_e} = 1.5 \times {10^{11}}\,m$, that of Mars orbit ${a_m} = 2.28 \times {10^{11}}\,m$, taken Kepler’s laws, the estimate of time of Mangalyaan to reach from earth to be close to:

(A) $500$ days
(B) $320$ days
(C) $260$ days
(D) $220$ days

Answer 1

By using Kepler's law, the estimate of time of Mangalyaan to reach from the earth is determined. But in Kepler’s law the radius of the circular path is required, so the radius is determined by equating the radius of the circle to be equal to the path covered by the ellipse. Because the semi major and semi minor axis of the ellipse is the only information we have.

Formula Used:
The Kepler’s law of planetary motion is given by,
${T^2} \propto {r^3}$
Where, $T$ is the time period and $r$ is the radius of the circular orbit.

Complete step by step answer:
Given that,
The semi major axis of the Earth’s orbit is, ${a_e} = 1.5 \times {10^{11}}\,m$,
The semi major axis of the mars orbit is, ${a_m} = 2.28 \times {10^{11}}\,m$.
Now, the total semi major axis is given by,
$\Rightarrow$ $a = \dfrac{{{a_e} + {a_m}}}{2}$
By substituting the semi major axis of the earth and the semi major axis of the mars in the above equation, then
$\Rightarrow$ $a = \dfrac{{\left( {1.5 \times {{10}^{11}}} \right) + \left( {2.28 \times {{10}^{11}}} \right)}}{2}$
By adding the terms in the numerator, then the above equation is written as,
$\Rightarrow$ $a = \dfrac{{3.78 \times {{10}^{11}}}}{2}$
On dividing the above equation, then
$\Rightarrow$ $a = 1.89 \times {10^{11}}\,m$
The semi major axis is, $a = 1.89 \times {10^{11}}\,m$
Now, the semi minor axis is assumed to be, $b \simeq {a_e} = 1.5 \times {10^{11}}\,m$
Consider that the circle whose area is equal to the path covered by the ellipse, then
$\Rightarrow$ $\pi {R^2} = \dfrac{{\pi ab}}{2}$
By cancelling the same terms on both sides, then
$\Rightarrow$ ${R^2} = \dfrac{{ab}}{2}$
By taking the square root on both sides, then
$\Rightarrow$ $R = \sqrt {\dfrac{{ab}}{2}}$
Substituting the semi major and semi minor axis values in the above equation, then
$\Rightarrow$ $R = \sqrt {\dfrac{{1.89 \times {{10}^{11}} \times 1.5 \times {{10}^{11}}}}{2}}$
On multiplying the above equation, then
$\Rightarrow$ $R = \sqrt {\dfrac{{2.835 \times {{10}^{22}}}}{2}}$
On dividing the above equation, then
$\Rightarrow$ $R = \sqrt {1.4175 \times {{10}^{22}}}$
By taking the square root on both sides, then
$\Rightarrow$ $R = 1.19 \times {10^{11}}\,m$
By using the Kepler’s law,
$\Rightarrow$ ${T^2} \propto {r^3}$
The above equation is written as,
$\Rightarrow$ ${\left( {\dfrac{T}{{365}}} \right)^2} = {\left( {\dfrac{R}{{{a_e}}}} \right)^3}\,....................\left( 1 \right)$
By substituting values in the above equation, then
$\Rightarrow$ ${\left( {\dfrac{T}{{365}}} \right)^2} = {\left( {\dfrac{{1.19 \times {{10}^{11}}}}{{1.5 \times {{10}^{11}}}}} \right)^3}$
By cancelling the same terms, then
$\Rightarrow$ ${\left( {\dfrac{T}{{365}}} \right)^2} = {\left( {\dfrac{{1.19}}{{1.5}}} \right)^3}$
On dividing the terms in RHS, then
$\Rightarrow$ ${\left( {\dfrac{T}{{365}}} \right)^2} = {\left( {0.793} \right)^3}$
Taking cube on RHS, then
$\Rightarrow$ ${\left( {\dfrac{T}{{365}}} \right)^2} = 0.499$
By keeping $T$ on one side and the other terms in other side, then
$\Rightarrow$ ${T^2} = 0.499 \times {\left( {365} \right)^2}$
On squaring and multiplying the terms in RHS, then
$\Rightarrow$ ${T^2} = 66520.09$
By taking square root on both sides, then
$\Rightarrow$ $T = 257.9$
The above equation is written as,
$T \simeq 260\,days$
Hence, the option (C) is the correct answer.

Note: In the equation (1), the time period is divided by the $365$ days because it is the days of one year and the radius is divided by the ${a_e}$ because it is the semi minor axis and also for the easy and the further calculation. And after by simplifying the time taken is determined.