Question

In young's experiment, the upper slit is covered by a thin glass plate of refractive index $\frac{4}{3}$ and of thickness $9\lambda$, where $\lambda$ is the wavelength of light [in air] used in the experiment. The lower slit is also covered by another glass plate of thickness $2\lambda$ & refractive index $\frac{3}{2}$, as shown in figure. If $I_0$ is the intensity at point P due to slits $S_1$ & $S_2$ each, then:

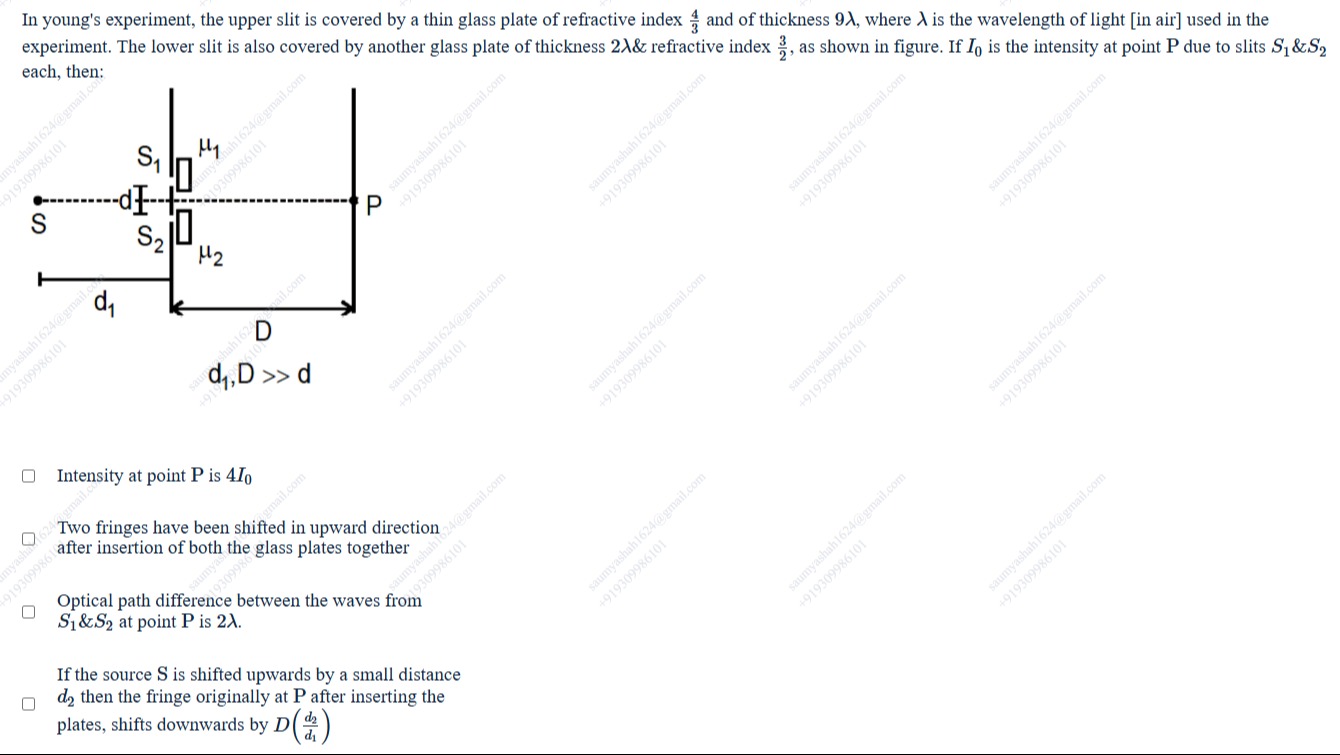
• A. Intensity at point P is $4I_0$
• B. Two fringes have been shifted in upward direction after insertion of both the glass plates together
• C. Optical path difference between the waves from $S_1$ & $S_2$ at point P is $2\lambda$.
• D. If the source S is shifted upwards by a small distance $d_2$ then the fringe originally at P after inserting the plates, shifts downwards by $D(\frac{d_2}{d_1})$

Answer 1

Answer: (A), (C), (D)

Options 1, 3, and 4 are correct.

Answer 2

Solution:

1. Extra Optical Path:
   When a glass plate of thickness $t$ and refractive index $\mu$ is inserted, the extra path compared to air is $(\mu-1)t$.

   • For the upper slit (S₁): $$\Delta_1=(\frac{4}{3}-1)\cdot 9\lambda = \frac{1}{3}\cdot9\lambda = 3\lambda.$$
   • For the lower slit (S₂): $$\Delta_2=(\frac{3}{2}-1)\cdot 2\lambda = \frac{1}{2}\cdot2\lambda = \lambda.$$

   Thus, the net extra path difference is:

   $$\Delta=\Delta_1-\Delta_2=3\lambda-\lambda=2\lambda.$$

   This extra path difference ($2\lambda$) produces a phase difference of

   $$\frac{2\lambda}{\lambda}\times 2\pi = 4\pi,$$

   which is equivalent to zero phase (i.e. constructive interference).

2. Intensity at Point P:
   With each slit producing intensity $I_0$ and the waves being in phase, the resultant amplitude adds, so:

   $$I_{\text{total}}=(\sqrt{I_0}+\sqrt{I_0})^2= (2\sqrt{I_0})^2 = 4I_0.$$

3. Fringe Shift Due to Plates:
   The extra path difference $\Delta=2\lambda$ would require a geometrical compensation of $2\lambda$ for the central maximum. In our geometry, the condition for constructive interference becomes:

   $$\delta_{\text{geom}} + 2\lambda = m\lambda.$$

   For $m=0$ (the new central fringe) we get:

   $$\delta_{\text{geom}} = -2\lambda,$$

   meaning the central maximum shifts from its original position. Since the extra delay is greater in the upper slit (S₁), the compensation is achieved by moving the point on the screen opposite to S₁, i.e. downward rather than upward. So the statement that "Two fringes have been shifted in upward direction" is incorrect.

4. Effect of Shifting Source S:
   In Young’s experiment, if the source S is moved vertically by a small displacement $d_2$ (with $d_1$ being the distance from the source to the slit plane), the fringe pattern on the screen shifts in the opposite direction by an amount proportional to $\frac{D\,d_2}{d_1}$ (where $D$ is the slit-screen distance). Hence, after the plate insertion, if S is shifted upward by $d_2$, the fringe originally at point P shifts downward by $D\left(\frac{d_2}{d_1}\right)$.