Question

In Young’s double-slit experiment with slit separation 0.1mm, one observes a bright fringe at an angle $\dfrac{1}{40}rad$ by using the light of wavelength ${{\lambda }_{1}}$. When the light of wavelength ${{\lambda }_{2}}$ is used a bright fringe is seen at the same angle in the same setup. Given that the ${{\lambda }_{1}}$ and ${{\lambda }_{2}}$ are in the visible range (380nm and 740nm) their values are
a) 380nm, 500nm
b) 625nm, 500nm
c) 380nm, 525nm
d) 400nm, 500nm

Answer 1

It is given in the question that the position of the bright fringe is the same for both the wavelengths of light used. It is also mentioned that the wavelengths i.e. ${{\lambda }_{1}}$ and ${{\lambda }_{2}}$ both lie in the visible spectrum. Hence we will use the condition for the angular position of bright fringe for a general wavelength in the above set up such that they have the same angular position, in order to determine the numerical value of their individual wavelengths.

Complete step-by-step solution:
Let us first take a wavelength of light $\lambda$ in general and see for what value of $\lambda$ lies in the visible spectrum forming a bright fringe the above set up.
The angular position for a bright fringe in Young’s double slit experiment is given by,
${{\theta }_{n}}=\dfrac{n\lambda }{d}....\text{(1),where n represents the }{{\text{n}}^{\text{th}}}\text{bright fringe, } \\!\\!\lambda\\!\\!\text{ is the wavelength of light used and d is the width of the slit}\text{.}$

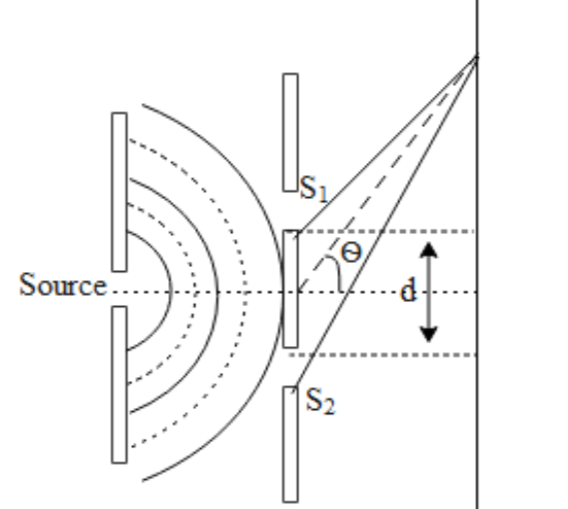
The above source represents in brief about Young’s double-slit experiment.
We know that the bright fringe is formed at an angle of $\dfrac{1}{40}rad$ and the slit width d is 0.1mm. let us substitute this equation 1 and we will get,
$\begin{aligned} & {{\theta }_{n}}=\dfrac{n\lambda }{d} \\\ & \dfrac{1}{40}=\dfrac{n\lambda }{0.1\times {{10}^{-3}}m} \\\ \end{aligned}$
$\begin{aligned} & n\lambda =0.25\times {{10}^{-5}}m \\\ & \lambda =\dfrac{2500\times {{10}^{-9}}m}{n}=\dfrac{2500 nm}{n} \\\ \end{aligned}$
Now let us substitute the value of n for $n^{th}$ bright fringe in order to determine the value of $\lambda$ which lies in the visible spectrum.
For n=1, $\lambda$=2500nm.
n=2, $\lambda$=1250nm
n=3, $\lambda$=833.3nm
n=4, $\lambda$=625nm
n=5, $\lambda$=500nm
n=6, $\lambda$=416.6nm
n=7, $\lambda$=357.14nm.
If we consider the above bright fringes, the ${{4}^{th}}$, ${{5}^{th}}$ and ${{6}^{th}}$ lies in the visible spectrum for their respective wavelengths for the above setup of Young’s double-slit experiment. The ${{6}^{th}}$ fringe formed by the wavelength of light used is not given in the options and hence the correct answer is the ${{4}^{th}}$and${{5}^{th}}$ bright fringe having their corresponding wavelengths as 625nm and 500nm.
Hence the correct answer is option b.

Note: The wavelengths of light 625nm and 500nm, will form a bright fringe which will overlap with each other. But the difference between them is that for the wavelength of light i.e. 625nm it will be its ${{4}^{th}}$ bright fringe. And for the wavelength of light i.e. 500nm, it will be it’s ${{5}^{th}}$ bright fringe.