Question

In Young’s double slit experiment using mono-chromatic light of wavelength $\lambda$, the intensity of light at a point on the screen where the path difference is $\lambda$, is $K$ units. Find out the intensity of light at a point where path difference is $\dfrac{2\lambda}{3}$

Answer 1

Young’s double slit experiment explains the wave nature of light using the interference of the light waves coming from two slits. The distance between the two slits is comparable to the magnitude of the wavelength.

Formula used:
$I=4I_{0} cos^{2}\left(\dfrac{\theta}{2}\right)$

Complete step by step answer:
In Young's double slit experiment; the distance between the two coherent sources is comparable to the wavelength. Due to the path difference between the light coming from both the slits, interference pattern is observed at the screen which is placed away from the sources.

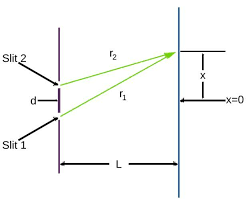
The path difference is given as $\Delta x=\dfrac{xd}{D}$, where $x$ is the position of the fringe from the origin, $d$ is the distance between the fringes and $D$ is the distance between the slits and source. Then the phase difference is given as $\theta=2\pi\dfrac{path\; difference }{\lambda}$
The final intensity of the wave $I$ is given as $I=I_{1}+I_{2}+2\sqrt{I_{1}I_{2}}cos\theta$ where $I_{1}$ and $I_{2}$ are the intensities of the incident light and $\theta$ is the phase difference between them. For a monochromatic light, $I_{1}=I_{2}=I_{0}$ then the total intensity $I=2I_{0}+2I_{0} cos\theta=2I_{0}(1+cos\theta)=2I\left(2cos^{2}\left(\dfrac{\theta}{2}\right)\right)=4I_{0} cos^{2}\left(\dfrac{\theta}{2}\right)$
Here, it is given that the path difference is $\lambda$ then the phase difference$\theta=2\pi$, the intensity is given as $I_{0}=K$
Let $I\prime$ be the total intensity at path difference$\dfrac{2\lambda}{3}$, then the phase difference $\theta=\dfrac{2\pi}{\lambda}\times \dfrac{2\lambda}{3}=\dfrac{4\pi}{3}$
Then the total intensity will become $I\prime=4K cos^{2}\left(\dfrac{4\pi}{3}\right)=4K\left(\dfrac{1}{4}\right)=K$
Thus the intensity of light at a point where path difference is $\dfrac{2\lambda}{3}$ is $K$

Note:
Constructive interference pattern occurs when the troughs or the crests of the two coherent sources interfere. These results in addition to their amplitude, hence the fringe is bright, or has more intensity. Similarly, Destructive interference pattern occurs when one trough and one crest of the two coherent sources interfere. These results in decreasing their amplitude, hence the fringe is dark, or has less intensity.